Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Δ=(2m-2)^2-4(2m-5)
=4m^2-8m+4-8m+20
=4m^2-16m+24
=4m^2-16m+16+8=(2m-4)^2+8>=8>0 với mọi m
=>Phương trình luôn có hai nghiệm phân biệt
\(B=\dfrac{x_1^2}{x^2_2}+\dfrac{x_2^2}{x_1^2}\)
\(=\dfrac{x_1^4+x_2^4}{\left(x_1\cdot x_2\right)^2}=\dfrac{\left(x_1^2+x_2^2\right)^2-2\left(x_1\cdot x_2\right)^2}{\left(x_1\cdot x_2\right)^2}\)
\(=\dfrac{\left[\left(2m-2\right)^2-2\left(2m-5\right)\right]^2-2\left(2m-5\right)^2}{\left(2m-5\right)^2}\)
\(=\dfrac{\left(4m^2-8m+4-4m+10\right)^2}{\left(2m-5\right)^2}-2\)
\(=\left(\dfrac{4m^2-12m+14}{2m-5}\right)^2-2\)
\(=\left(\dfrac{4m^2-10m-2m+5+9}{2m-5}\right)^2-2\)
\(=\left(2m-1+\dfrac{9}{2m-5}\right)^2-2\)
Để B nguyên thì \(2m-5\in\left\{1;-1;3;-3;9;-9\right\}\)
=>\(m\in\left\{3;2;4;1;7\right\}\)

Đáp án cần chọn là: C
Vì nn nguyên dương nên để 6 n + 2 nguyên thì n + 2∈U(6) = {±1;±2;±3;±6}
Ta có bảng:

Vậy giá trị của n nguyên dương thỏa mãn là: n = 1;n = 4

Đáp án cần chọn là: A
Vì n nguyên dương nên để 9 4 n + 1 nguyên thì 4n + 1∈U(9) = {±1;±3;±9}
Ta có bảng:

Vậy có duy nhất một giá trị của n thỏa mãn là n = 2

Để \(\dfrac{a}{5}\) là số nguyên thì \(a⋮5\)
\(\Leftrightarrow a\in B\left(5\right)\)
\(\Leftrightarrow a\in\left\{0;5;10;15;...\right\}\)
mà a là số nguyên dương nhỏ nhất
nên a=5
Vậy: a=5

Chọn đáp án B
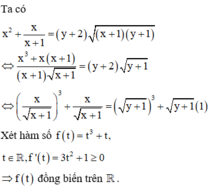
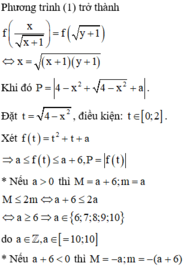
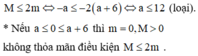
Vậy có 5 giá trị nguyên của m thỏa mãn điều kiện.

a) Để \(\frac{11}{\sqrt{x}-5}\)nhận giá trị nguyên thì \(\sqrt{\text{x}}-5\inƯ\left(11\right)\)(DK : \(0\le x\ne25\))
Vì \(\sqrt{\text{x}}-5\ge-5\)nên ta có :
\(\sqrt{x}-5\in\left\{-1;1;11\right\}\)\(\Rightarrow\sqrt{x}\in\left\{4;6;16\right\}\Rightarrow x\in\left\{16;36;256\right\}\)
b) \(B=\frac{\sqrt{x}+1}{\sqrt{x}-3}=\frac{\sqrt{x}-3+4}{\sqrt{x}-3}=1+\frac{4}{\sqrt{x}-3}\)(DK : \(0\le x\ne9\))
Để B nhận giá trị nguyên thì \(\sqrt{x}-3\inƯ\left(4\right)\)
Vì \(\sqrt{\text{x}}-3\ge-3\)nên ta có :
\(\sqrt{\text{x}}-3\in\left\{-2;-1;1;2;4\right\}\)\(\Rightarrow\sqrt{x}\in\left\{1;2;4;5;7\right\}\Rightarrow x\in\left\{1;4;16;25;49\right\}\)