tìm x biết 2x3 + 3x2 + 2x + 3 = 0
help me!!! ai giải đc cho 2 like!!! 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
JP
1
Gửi bạn
DT
7 tháng 2 2022
Đặt d : deg P(x) , ta có:
\(4=d^2\Leftrightarrow d=2\)
\(\Rightarrow P\left(x\right)=ax^2+bx+c\left(a\ne0\right)\)
Trog đó , hệ số cao nhất của vế trái là 1 nên a=1 . thay vào và thu gọn 2 vế đc:
\(x^4+2x^3+6x^2-8x+8=x^4+bx^3+\left(4+c\right).x^2+4bx+4c\)
Tiến hành đồng nhất, ta được:
\(\left\{{}\begin{matrix}b=-2\\c=2\end{matrix}\right.\)
suy ra: \(P\left(x\right)=x^2-2x+2\)
LP
7 tháng 2 2022
Đặt d : deg P(x) , ta có:
4=d2⇔d=24=d2⇔d=2
⇒P(x)=ax2+bx+c(a≠0)⇒P(x)=ax2+bx+c(a≠0)
Trong đó , hệ số cao nhất của vế trái là 1 nên a=1 . thay vào và thu gọn 2 vế đc:
x^4+2x^3+6x^2−8x+8=x^4+bx^3(4+c).x^2+4bx+4c
Tiến hành đồng nhất, ta được:
{ b=-2 c=2
suy ra: P(x)=x^2−2x+2
mình chỉ bít zậy ko biết có đúng không nữa 
C
1
3 tháng 10 2021
a: Ta có: \(2\left(x-2\right)^3=2-x\)
\(\Leftrightarrow2\left(x-2\right)^3+x-2=0\)
\(\Leftrightarrow x-2=0\)
hay x=2
b: ta có: \(8x^3-72x=0\)
\(\Leftrightarrow x\left(x-3\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=3\\x=-3\end{matrix}\right.\)
c: Ta có: \(2x^3+3x^2+2x+3=0\)
\(\Leftrightarrow2x+3=0\)
hay \(x=-\dfrac{3}{2}\)
25 tháng 9 2021
1) \(\Leftrightarrow\left(x-4\right)\left(x+4\right)-x\left(x-4\right)=0\)
\(\Leftrightarrow\left(x-4\right)\left(x+4-x\right)=0\)
\(\Leftrightarrow\left(x-4\right)4=0\)
\(\Leftrightarrow x=4\)
2) \(\left(x+3\right)^2-\left(x-3\right)\left(x+5\right)=x^2+6x+9-x^2-2x+15=4x+24\)
3) \(2x^3+3x^2-2x+a=2x^2\left(x-2\right)+7x\left(x-2\right)+16\left(x-2\right)+32+a\)
Để \(2x^3+3x^2-2x+a⋮x-2\) thì \(32+a=0\Leftrightarrow a=-32\)
HP
25 tháng 9 2021
1.
x2 - 16 - x(x - 4) = 0
<=> (x2 - 42) - x(x - 4) = 0
<=> (x - 4)(x + 4) - x(x - 4) = 0
<=> (x + 4 - x)(x + 4) = 0
<=> 4(x + 4) = 0
<=> x + 4 = 0
<=> x = -4
2.
(x + 3)2 - (x - 3)(x + 5)
= x2 + 6x + 9 - (x2 + 5x - 3x - 15)
= x2 + 6x + 9 - x2 + 5x - 3x - 15
= x2 - x2 + 6x + 5x - 3x + 9 - 15
= 8x - 6
CM
11 tháng 2 2019
Đặt và thực hiện phép tính ta có :
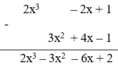
Vậy chọn đa thức thứ hai.
29 tháng 8 2023
b: 4x^2-20x+25=(x-3)^2
=>(2x-5)^2=(x-3)^2
=>(2x-5)^2-(x-3)^2=0
=>(2x-5-x+3)(2x-5+x-3)=0
=>(3x-8)(x-2)=0
=>x=8/3 hoặc x=2
c: x+x^2-x^3-x^4=0
=>x(x+1)-x^3(x+1)=0
=>(x+1)(x-x^3)=0
=>(x^3-x)(x+1)=0
=>x(x-1)(x+1)^2=0
=>\(x\in\left\{0;1;-1\right\}\)
d: 2x^3+3x^2+2x+3=0
=>x^2(2x+3)+(2x+3)=0
=>(2x+3)(x^2+1)=0
=>2x+3=0
=>x=-3/2
a: =>x^2(5x-7)-3(5x-7)=0
=>(5x-7)(x^2-3)=0
=>\(x\in\left\{\dfrac{7}{5};\sqrt{3};-\sqrt{3}\right\}\)
11 tháng 2 2020
Chết mẹ nhầm; đề đây nha:
Tìm m sao cho với mọi x, ta có: 2x3−3x2+x+m=(x+2)(2x2 -7x+15)
11 tháng 2 2020
Bài giải:
Cách 1: Ta có
(x+2)(2x2−7x+15)
=2x3−7x2+15x+4x2−14x+30
=2x3−3x2+x+30
Vì 2x3−3x2+x+m=2x3−3x2+x+30⇒m=30.
Cách 2: Cho x=−2 thì vế phải bằng 0. Khi đó vế trái bằng m−30. Do đó m = 30. Thử lại thấy thỏa mãn.
\(2x^3+3x^2+2x+3=0\)
\(\Leftrightarrow\left(2x^3+2x\right)+\left(3x^2+3\right)=0\)
\(\Leftrightarrow2x\left(x^2+1\right)+3\left(x^2+1\right)=0\)
\(\Leftrightarrow\left(x^2+1\right)\left(2x+3\right)=0\)
\(\Leftrightarrow2x+3=0\) (Vì \(x^2+1>0\))
\(\Leftrightarrow x=-\frac{3}{2}\)
\(2x^3+3x^2+2x+3=0\)
\(\Rightarrow\left(2x^3+2x\right)+\left(3x^2+3\right)=0\)
\(\Rightarrow\left[2x.\left(x^2+1\right)\right]+\left[3.\left(x^2+1\right)\right]=0\)
\(\Rightarrow\left(x^2+1\right)\left(3+2x\right)=0\)
Suy ra:\(\begin{cases}x^2+1=0\\3+2x=0\end{cases}\)\(\Rightarrow\begin{cases}x\in\varnothing\\x=\frac{-3}{2}\end{cases}\)
Vậy \(x=-\frac{3}{2}\)