cho hàm số y=f(x) vs công thức 5 trên x-1
tìm các giá trị của x để vế phải của công thức có nghĩa
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
21 tháng 7 2017
Hàm số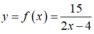 
có nghĩa khi 2x - 4 ≠ 0 ⇒ 2x ≠ 4 ⇒ x ≠ 2
Chọn đáp án D
TT
1
\(x\ne1\)
công thức có nghĩa \(\Leftrightarrow\frac{5}{x-1}\ne0\Leftrightarrow x-1\ne0\Leftrightarrow x\ne1\)