a) Thu gọn biểu thức sau: A = \(\frac{2-\sqrt{3}}{1+\sqrt{4+2\sqrt{3}}}\) + \(\frac{2+\sqrt{3}}{1-\sqrt{4-2\sqrt{3}}}\)
b) Ông Sáu gửi một số tiền vào ngân hàng theo mức lãi xuất tiết kiệm với kỳ hạn 1 năm là 6%. Tuy nhiên sau thời hạn một năm ông Sáu không đến nhận tiền lãi mà để thêm 1 năm nữa mới lãnh. Khi đó số tiền lãi có được sau năm đầu tiên sẽ được ngân hàng cộng dồn vào số tiền gửi ban đầu để thành số tiền gửi ch năm kế tiếp với mức lãi suất cũ. Sau 2 năm ông Sáu nhận được số tiền là 112.360.000 đồng (kể cả gốc lẫn lãi). Hỏi ban đầu ông Sáu đã gửi bao nhiêu tiền?

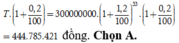
a) \(A=\frac{2-\sqrt{3}}{1+\sqrt{4+2\sqrt{3}}}+\frac{2+\sqrt{3}}{1-\sqrt{4-2\sqrt{3}}}\)
\(=\frac{2-\sqrt{3}}{1+\sqrt{\left(\sqrt{3}+1\right)^2}}+\frac{2+\sqrt{3}}{1-\sqrt{\left(\sqrt{3}-1\right)^2}}\)
\(=\frac{2-\sqrt{3}}{1+\sqrt{3}+1}+\frac{2+\sqrt{3}}{1-\sqrt{3}+1}\)
\(=\frac{2-\sqrt{3}}{2+\sqrt{3}}+\frac{2+\sqrt{3}}{2-\sqrt{3}}\)
\(=\frac{\left(2-\sqrt{3}\right)\left(2-\sqrt{3}\right)+\left(2+\sqrt{3}\right)\left(2+\sqrt{3}\right)}{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}\)
\(=\frac{4-4\sqrt{3}+3+4+4\sqrt{3}+3}{4-3}\)
\(=14\)
a) A = \(\frac{2-\sqrt{3}}{1+\sqrt{4+2\sqrt{3}}}\) + \(\frac{2+\sqrt{3}}{1-\sqrt{4-2\sqrt{3}}}\) = \(\frac{2-\sqrt{3}}{1+\sqrt{3+2\sqrt{3.1+1}}}\) + \(\frac{2+\sqrt{3}}{1-\sqrt{3-2\sqrt{3.1+1}}}\) = \(\frac{2-\sqrt{3}}{1+\sqrt{\left(\sqrt{3+1}\right)^2}}\) + \(\frac{2+\sqrt{3}}{1-\sqrt{\left(\sqrt{3-1}\right)^2}}\) = \(\frac{2-\sqrt{3}}{1+\sqrt{3+1}}\) + \(\frac{2+\sqrt{3}}{1-\sqrt{3+1}}\) = \(\frac{2-\sqrt{3}}{2+\sqrt{3}}\) + \(\frac{2+\sqrt{3}}{2-\sqrt{3}}\) = \(\frac{\left(4-4\sqrt{3+3}\right)+\left(4+4\sqrt{3+3}\right)}{4-3}\) = \(\frac{14}{1}\) = 1