Hai vật dao động điều hòa dọc theo các trục song song với nhau. Phương trình dao động các vật lần lượt là x1=A1coswt (cm) và x2=A2sinwt. Biết 64x12+36x22 =482 (cm). Tại thời điểm t, vật thứ nhất đi qua vị trí có li độ x1=3cm với vận tốc v1=-18cm/s. Khi đó vật thứ hai có tốc độ bằng bao nhiêu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
+ Thay x1 = 3cm vào ![]() => x2 = ± 4cm.
=> x2 = ± 4cm.
+ Đạo hàm theo thời gian hai vế của phương trình ![]() , ta được:
, ta được:
64. 2x1v1 + 36.2x2v2 = 0 (v chính là đạo hàm bậc nhất của x theo thời gian).
Hay 128.x1v1 + 72.x2v2 = 0. Thay giá trị của x1, x2 và v1 vào ta được |v2|= 24 cm/s.

Đáp án D
+ Từ phương trình : 64 x 1 2 + 36 x 2 2 = 48 2 c m (1) Thay x 1 = 3 cm, ta có:
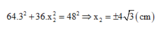
+ Đạo hàm phương trình (1), ta có:
![]()
⇒ 64 . 2 x 1 . x 1 ' + 36 . 2 x 2 . x 2 ' = 0 ⇒ 128 x 1 . x 1 ' + 72 x 2 . x 2 ' = 0
+ Theo định nghĩa vận tốc, ta có: v = x ' = ⇒ x 1 ' = v 1 x 2 ' = v 2
Thay vào phương trình trên ta có: 128 x 1 . v 1 + 72 x 2 . v 2 = 0 ⇒ v 2 = - 128 x 1 . v 1 72 x 2
+ Về độ lớn (tốc độ):
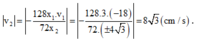

Đáp án D
+ Từ phương trình: 64 x 1 2 + 36 x 2 2 = 48 2 1 . Thay x 1 = 3 cm, ta có:
64 .3 2 + 36 . x 2 2 = 48 2 ⇒ x 2 = ± 4 3 cm
+ Đạo hàm phương trình (1), ta có:
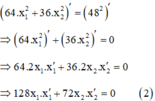
+ Theo định nghĩa vận tốc, ta có: v = x ' ⇒ x ' 1 = v 1 x ' 2 = v 2
Thay vào phương trình trên ta có: 128 x 1 . v 1 + 72 x 2 . v 2 = 0 ⇒ v 2 = − 128 x 1 . v 1 72 x 2
+ Về độ lớn (tốc độ):
v 2 = − 128 x 1 . v 1 72 x 2 = − 128 .3. − 18 72 . ± 4 3 = 8 3 cm / s

Đạo hàm: 64 x 1 2 + 32 x 2 2 = 48 2 (*)
→ 128 x 1 v 1 + 64 x 2 v 2 = 0 (**)
Tại thời điểm t: x 1 = 3cm, từ (*) → x 2 = 3 6 , theo (**) → x 2 = 6 6 cm/s.
Chọn C.
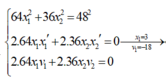
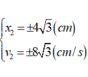
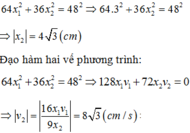
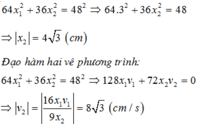
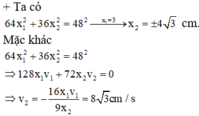


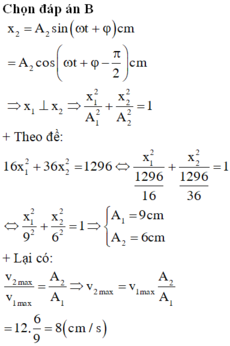
Ta có :
\(64^2_1x=36x^2_2=48^2\)
=> \(64x_1\le48^2\)
=> \(36x_2\le48^2\)
=> A1 = 6 (cm)
=> A2 = 8 (cm)
=> \(\frac{V_2}{V_1}=\frac{\omega\sqrt{A^2_2-x^2_2}}{\omega\sqrt{A^2_1-x^2_1}}=\frac{\sqrt{A^2_2-x^2_2}}{\sqrt{A^2_1-x^2_1}}=\frac{4}{3\sqrt{3}}\)
Vậy V2 = \(\frac{4.18}{3\sqrt{3}}=8\sqrt{3}\) (cm/giây)