cho hai đường thẳng x'x và y'y cắt nhau tại điểm O. biết xOy=30 độ. vẽ tia Ot vuông góc với xx' , Ot' vuông góc với yy' sao cho Ot và Ot' thuộc nửa mặt phẳng bờ xx' chứa tia Oy. Số đo của tOt' là...............
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a,Góc xÔy => xÔy đối đỉnh x'Ôy' <=> xÔy = x'Ôy' = 100o
Ta có xÔy + yÔx' = xÔx' (kề bù)
100o + yÔx' = 180o
yÔx' = 180o - 100o
yÔx' = 80o
=> yÔx' đối đỉnh xÔy' <=> yÔx' = xÔy' = 80o

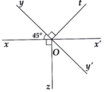
a) Vì Oy' là phân giác x ' O z ^ nên
x ' O y ' ^ = 1 2 x ' O z ^ = 1 2 . 90° = 45°
=> x O y ^ = x ' O y ' ^
Mà Ox và Ox' là hai tia đối nhau nên
x O y ^ và x ' O y ' ^ đối đỉnh
b) x ' O y ^ = 45°, y ' O t ^ = 90° => Ox' là phân giác t O y ' ^
Do đó x ' O t ^ = 45°

a) (Sửa lại là xOy và x'Oy' đối đỉnh nha, k có t trog đề bài ![]() )
)
Ta có : \(\widehat{x'Oy}=180^o-\widehat{xOy}=180^o-45^o=135^o\)
Oy là tia phân giác của góc x'Oy' nên \(\widehat{x'Oy'}=\frac{1}{2}\widehat{x'Oz}=\frac{1}{2}.90^o=45^o\)
Do đó \(\widehat{x'Oy}+\widehat{x'Oy'}=135^o+45^o=180^o\) => Oy, Oy' là 2 tia đối nhau (1)
; đã có điểm O trên đg thẳng xx' nên Ox, Ox' đối nhau (2)
Từ (1) và (2) => góc xOy và x'Oy' đối đỉnh
b) Ta có : \(\widehat{xOy}+\widehat{yOt}+\widehat{x'Ot}=180^o\) (kề bù)
=> \(\widehat{x'Ot}=180^o-45^o-90^o=45^o\)

sai đề rồi hai góc kề bù tạo bởi hai tia đối nhau có tổng số đo bằng 180o
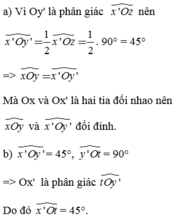
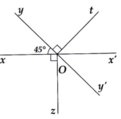
+) Ta có: xOy + xOt' = yOt'
=> 300 + xOt' = 900
=> xOt' = 900 - 300
=> xOt' = 600
+) Ta có: xOt' + tOt' = xOt
=> 600 + tOt' = 900
=> tOt' = 900 - 600
=> tOt' = 300
Vậy tOt' = 300
Chuk bạn hok tốt !