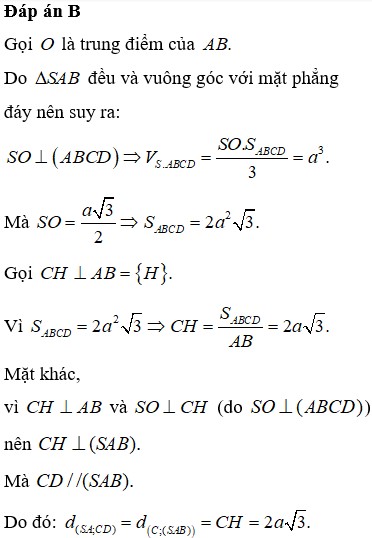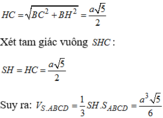cho hình chóp sabcd có đáy là hình vuông cạnh a, SA vuông góc với đáy, góc giữa SC và (SAB) bằng 45. Gọi G là trọng tâm tam giác SAB. tính thể tích khối chóp GABCD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
Nguyễn Thị Anh
18 tháng 6 2016
Đúng(0)
Những câu hỏi liên quan
CM
25 tháng 8 2017
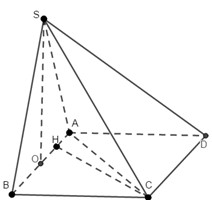
Đáp án B
Gọi H là chân đường vuông góc hạ từ đỉnh S lên mặt phẳng (ABC), khi đó ta chứng minh được H là trung điểm của BC. Gọi M là trung điểm của AB khi đó từ giả thiết ta có: 
Đặt AB = x ta tính được: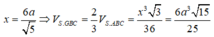 
HP
17 tháng 6 2021
Kẻ SH vuông góc AB tại H.
a, Ta có: \(h=SH=AH.tan\alpha=2a\)
\(\Rightarrow V=\dfrac{1}{3}.B.h=\dfrac{1}{3}.\left(2a\right)^2.2a=\dfrac{8a^3}{3}\)
b, \(SB=BC.tan\alpha=2\sqrt{5}a\Rightarrow SH=\sqrt{SB^2-BH^2}=\sqrt{19}a\)
\(\Rightarrow V=\dfrac{1}{3}.B.h=\dfrac{1}{3}.\left(2a\right)^2.\sqrt{19}a=\dfrac{4\sqrt{19}a^3}{3}\)
c, Kẻ HI vuông góc với CD.
Ta có: \(SH=HI.tan\alpha=6a\)
\(\Rightarrow V=\dfrac{1}{3}.B.h=\dfrac{1}{3}.\left(2a\right)^2.6a=8a^3\)
AH
Akai Haruma
Giáo viên
22 tháng 6 2021
Lời giải:
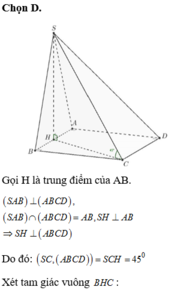
Lấy $H$ là trung điểm $AB$ thì do $SAB$ cân tại $S$ nên $SH\perp BH$
$BH$ là giao tuyến của $(SAB), (ABCD)$; (SAB)\perp (ABCD)$ nên $SH\perp (ABCD)$
$\Rightarrow (SC, (ABCD))=(SC, CH)=\widehat{SCH}=45^0$
$\Rightarrow SH=CH=\sqrt{BC^2+BH^2}=\sqrt{(2a)^2+(\frac{a}{2})^2}=\frac{\sqrt{17}}{2}a$
\(V_{S.ABCD}=\frac{1}{3}.SH.S_{ABCD}=\frac{1}{3}.\frac{\sqrt{17}}{2}a.a.2a=\frac{\sqrt{17}}{3}a^3\)
