Một quả cầu m = 8kg buộc vào đầu một lò xo nhẹ có thể chuyển động không ma sát trên mặt phẳng nằm ngang, đầu kia của lò xo gắn vào điểm cố định, chọn gốc thế năng là vị trí đầu lò xo gắn với vật nặng khi chưa biến dạng. Nén lò xo lại một đoạn rồi thả thấy khi lò xo qua vị trí bị nén 8 cm đối với chiều dài tự nhiên thì vận tốc của vật nặng là 1,6 m/s và động năng bằng bốn lần thế năng đàn hồi. Độ cứng của lò xo bằng:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ \(W=\dfrac{1}{2}kx^2+\dfrac{1}{2}mv^2=\dfrac{1}{2}k\Delta l^2\)
\(\Leftrightarrow kx^2+mv^2=k\Delta l^2\Leftrightarrow v=\sqrt{\dfrac{k\Delta l^2-kx^2}{m}}=\sqrt{\dfrac{40.0,02^2-40x^2}{0,4}}\left(m/s\right)\)
b/ \(v_{max}\Leftrightarrow\dfrac{40.0,02^2-40x^2}{0,4}\left(max\right)\Leftrightarrow x=0\) => khi nó ở VTCB
\(\Rightarrow v_{max}=\dfrac{40.0,02^2}{0,4}\left(m/s\right)\)

Đáp án A
Ta có thể mô tả chuyển động của hệ hai vật thành các giai đoạn sau:
Giai đoạn 1: Hệ hai vật m 1 và m 2 dao động điều hòa quanh vị trí cân bằng (lò xo không biến dạng)
Tần số góc của dao động
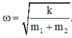
Tốc độ của hệ tại vị trí cân bằng
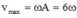
Giai đoạn 2: Vật m 2 tách ra khỏi m 1 chuyển động thẳng đều với vận tốc v m a x , vật m 1 dao động điều hòa quanh vị trí cân bằng cũ.
Biên độ dao động của m 1 :
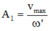
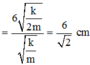
Khi lò xo có chiều dài lớn nhất → vật m 1 chuyển động ra biên, m 2 chuyển động với khoảng thời gian tương ứng
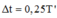
→ Khoảng cách giữa hai vật
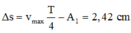

Giải thích: Đáp án B
Phương pháp: Vận tốc ở VTCB: v = ωA
Cách giải:
Khi về đến VTCB thì cả hai vật có vận tốc 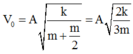
Sau đó vật m sẽ dao động với chu kỳ 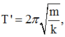 và biên độ
và biên độ 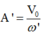
Vật M sẽ tiếp tục chuyển động thẳng đều với vận tốc V0
Ở thời điểm lò xo có chiều dài cực đại lần đầu tiên m đến vị trí biên A’, còn M đi được quãng đường là 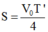
=> Khoảng cách giữa hai vật m và M là:d = S - A’=4,19cm.

Đáp án D
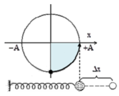
Vật m2 sẽ tác dụng ra khỏi vật m1 tại vị trí cân bằng của hệ bởi tại vị trí này:
+) Vật m1 có tốc độ cực đại và bắt đầu giảm
+) Vật m2 sẽ tiếp tục chuyển động thẳng đều với tốc độ bằng tốc độ cực đại
Lò xo có độ dài cực đại là đầu tiên ứng với khoảng thời gian T/4, khi đó Khoảng cách giữa hai vật là
∆ x = ω A T 4 - A = 4 , 6 c m

Hướng dẫn:
Giai đoạn 1: Hai vật dao động điều hòa với biên độ A = 8 cm quanh vị trí cân bằng O từ biên về vị trí cân bằng.
+ Tần số góc dao động của hệ ω = k m 1 + m 2 = k 2 m rad/s.
→ Khi hệ hai vật đến O, ta có v = v m a x = ω A = 8 ω c m / s .
Giai đoạn 1: Vật m1 dao động điều hòa quanh vị trí cân bằng O, vật m2 chuyển động thẳng đều ra xa với tốc độ v 2 = v m a x .
+ Tần số góc của con lắc sau khi vật m 2 tách ra khỏi m 1 ω ' = k m 1 = k m = 2 ω rad/s → T ' = 2 π 2 ω = 2 π ω s.
Tại vị trí vật m 2 tách khỏi vật m 1 , ta có x′ = 0, v ′ = v m a x .
→ Biên độ dao động mới của m 1 là A 1 = v m a x ω ' = 8 ω ω ' = 4 2 cm.
+ Lò xo giãn cực đại lần đầu tiên kể từ thời điểm hai vật tách nhau ứng với Δt = 0,25T s.
→ Khoảng cách giữa hai vật lúc đó là Δ x = x 2 − x 1 = v m a x T ' 4 − A 1 = 8 ω 2 π 4 ω − 4 2 = 3 , 22 cm.
Đáp án D




kiểu lớp 10
10
Theo bài ra ta có:
W=Wđ+Wt =1/2.m.v2 +1/2.k.x2= 5.1/2.k.x2
Khi wt =4wđ thì cơ năng ở đó là:
w=wđ+wt = 5/4.wt = 5/4.1/2.kx'2
Theo định luật bảo toàn cơ năng cho hai vị trí ta có:
5/4.1/2.kx'^2 = 5.1/2.k.x^2 -> x' = ...