nếu d cắt DE thì d có cắt AB không? Giải thích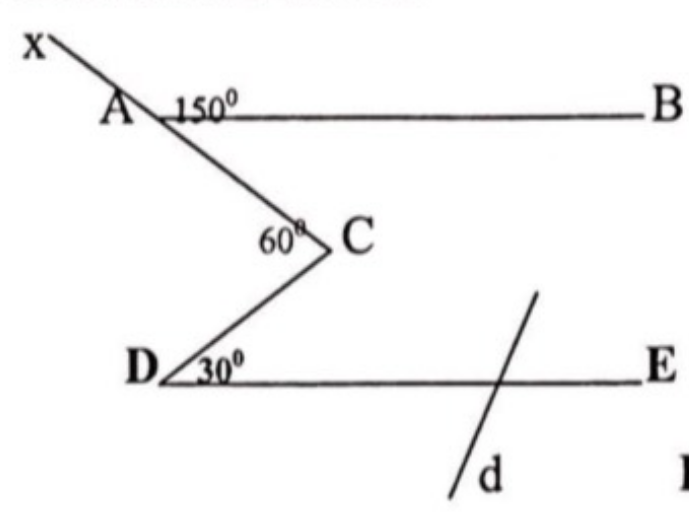
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có MD là phân giác ˆAMB
⇒AD/BD=AM/BM(1)
ME là phân giác ˆAMC
⇒AE/CE=AM/CM(2)
Mà MB=MC (AM là trung tuyến)
⇒AM/BM=AM/MC(3)
(1)(2)(3)⇒AD/BD=AE/CE
=> DE//BC (định lý Talet đảo)

a: Xét ΔAMB có MD là phân giác
nên AD/DB=AM/MB=AM/MC(1)
Xét ΔAMC có ME là phân giác
nên AE/EC=AM/MC(2)
Từ (1) và (2) suy ra AD/DB=AE/EC
hay DE//BC
b: MB=3cm
AD/DB=AM/MB=5/3
=>AD/DB=AE/EC=5/3
=>DB/AD=3/5
=>AD/AB=5/8
Xét ΔABC có DE//BC
nên AD/AB=DE/BC
=>DE/6=5/8
hay DE=3,75(cm)

a: Xét ΔMAB có MD là phân giác
nên AD/DB=AM/MB=AM/MC
Xét ΔMAC ó ME là phân giác
nên AE/EC=AM/MC=AD/DB
=>ED//BC
b: Xét ΔMAB có MD là phân giác
nên AD/DB=AM/MB=5/3
=>AD/AB=5/8
Xét ΔABC có DE//BC
nên DE/BC=AD/AB
=>DE/6=5/8
=>DE=3,75cm

c, Xét \(\Delta\)IEB và \(\Delta\)CAB có :
góc E = góc A (= 90o)
góc B - chung
AB = EB ( theo câu b)
=> hai tam giác trên bằng nhau (g.c.g) => IB=IC (cặp cạnh tương ứng)=> tam giác BIC cân tại B (đpcm)
d,Từ câu a, ta có: AB=BE => tam giác ABE cân tại B => góc BEA = góc BAE ( hai góc ở đáy)
=> góc B = 180o - ( góc AEB + góc EAB ) = 180o - 2 góc BEA (1)
Từ câu b, ta có: tam giác BIC cân tại B => góc I = góc C ( hai góc ở đáy)
=> góc B = 180o - ( góc I + góc C ) = 180o - 2 góc BCI (2)
Từ 1 và 2, ta được: góc BEA = góc BCI
mà hai góc này ở vị trí đồng vị => AE//IC (đpcm)

Suy ra d'//d'' vì
- Nếu d' cắt d'' tại điểm M thì M không nằm trên d vì d//d', d//d''
- Qua điểm M nằm ngoài d ta vẽ được hai đường thẳng d', d'' cùng song song với d. Điều này trái với tiên đề Oclit về đường thẳng song song
- Nên d' và d'' không thể cắt nhau. Vậy d'//d''
Có vì DE//AB