Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=x^3+y^3=\left(x+y\right)^3-3xy\left(x+y\right)=5^3-3.5.4=65\)

\(x+y=4=>\left(x+y\right)^2=16\)
\(=>x^3+y^3=\left(x+y\right)\left(x^2-xy+y^2\right)\)
\(=4\left(x^2+2xy+y^2-3xy\right)=4\left[\left(x+y\right)^2-3.3\right]=4\left(16-9\right)=28\)
Lời giải:
Theo hằng đẳng thức đáng nhớ:
$x^3+y^3=(x+y)^3-3xy(x+y)=4^3-3.3.4=28$

\(B=x^3-y^3+\left(x+y\right)^2\)
\(=\left(x-y\right)^3+3xy\left(x-y\right)+\left(x-y\right)^2+4xy\)
\(=4^3+3\cdot4\cdot5+4^2+4\cdot5\)
\(=160\)
\(\left(x+y\right)^2=\left(x-y\right)^2+4xy=4^2+4.5=36\)
\(x^3-y^3=\left(x-y\right)^3+3xy\left(x-y\right)=4^3+3.5.4=124\)
\(\Rightarrow B=124+36=160\)

a) \(11^3-1\)
\(=11^3-1^3\)
\(=\left(11-1\right)\left(11^2+11\cdot1+1^2\right)\)
\(=10\cdot\left(121+11+1\right)\)
\(=10\cdot\left(132+1\right)\)
\(=10\cdot133\)
\(=1330\)
b) Ta có:
\(x^3-y^3\)
\(=\left(x-y\right)^3+3xy\left(x-y\right)\)
Thay \(x-y=6\) và \(xy=20\) ta có:
\(6^3+3\cdot20\cdot6=216+60\cdot6=216+360=576\)
a: 11^3-1=(11-1)(11^2+11+1)
=10*(121+12)
=10*133=1330
b: x^3-y^3=(x-y)^3+3xy(x-y)
=6^3+3*20*6
=216+360
=576

\(x-y=1\Leftrightarrow x=1+y\\ P=\left(x-y\right)\left(x^2+xy+y^2\right)-xy\\ P=x^2+xy+y^2-xy\\ P=x^2+y^2=y^2+2y+1+y^2\\ P=2\left(y^2+y+\dfrac{1}{4}\right)+\dfrac{1}{2}=2\left(y+\dfrac{1}{2}\right)^2+\dfrac{1}{2}\ge\dfrac{1}{2}\)
Dấu \("="\Leftrightarrow y=-\dfrac{1}{2}\Leftrightarrow x=1-\dfrac{1}{2}=\dfrac{1}{2}\)

a) Ta thấy \(xy=\dfrac{\left(x+y\right)^2-\left(x^2+y^2\right)}{2}=\dfrac{3^2-5}{2}=2\)
\(\Rightarrow x^3+y^3=\left(x+y\right)\left(x^2+y^2-xy\right)\) \(=3\left(5-2\right)=9\)
b) Ta thấy \(xy=\dfrac{-\left(x-y\right)^2+\left(x^2+y^2\right)}{2}=\dfrac{15-5^2}{2}=-5\)
\(\Rightarrow x^3-y^3=\left(x-y\right)\left(x^2+y^2+xy\right)\) \(=5\left(15-5\right)=50\)

\(a,x+y=1\Leftrightarrow\left(x+y\right)^3=1\Leftrightarrow x^3+y^3+3xy\left(x+y\right)=1\\ \Leftrightarrow x^3+y^3+3xy\cdot1=1\Leftrightarrow x^3+y^3+3xy=1\)
\(b,x^3-y^3-3xy\\ =x^3-3x^2y+3xy^2-y^3-3xy+3x^2y-3xy^2\\ =\left(x-y\right)^3-3xy\left(x-y-1\right)\\ =1^3-3xy\left(1-1\right)=1-0=1\)
\(c,x^3+y^3+3xy\left(x^2+y^2\right)+6x^2y^2\left(x+y\right)\\ =\left(x+y\right)\left(x^2-xy+y^2\right)+3xy\left[\left(x+y\right)^2-2xy\right]+6x^2y^2\\ =x^2-xy+y^2+3xy-6x^2y^2+6x^2y^2\\ =x^2+2xy+y^2=\left(x+y\right)^2=1\)

\(a,x^4-2x^3+6x^2+x+14\\ =\left(x^4-3x^3+7x^2\right)+\left(x^3-3x^2+7x\right)+\left(2x^2-6x+14\right)\\ =\left(x^2-3x+7\right)\left(x^2+x+2\right):\left(x^2-3x+7\right)=x^2+x+2\)
Ta có \(x^2+x+2=x^2+x+\dfrac{1}{4}+\dfrac{7}{4}=\left(x+\dfrac{1}{2}\right)^2+\dfrac{7}{4}\ge\dfrac{7}{4}>0\)
Vậy ...
\(b,A=x^3+3xy+y^3\\ A=\left(x+y\right)\left(x^2-xy+y^2\right)+3xy\\ A=x^2-xy+y^2+3xy\\ A=x^2+2xy+y^2=\left(x+y\right)^2=1\)

Bài 5
a) A = -x³ + 6x² - 12x + 8
= -x³ + 3.(-x)².2 - 3.x.2² + 2³
= (-x + 2)³
= (2 - x)³
Thay x = -28 vào A ta được:
A = [2 - (-28)]³
= 30³
= 27000
b) B = 8x³ + 12x² + 6x + 1
= (2x)³ + 3.(2x)².1 + 3.2x.1² + 1³
= (2x + 1)³
Thay x = 1/2 vào B ta được:
B = (2.1/2 + 1)³
= 2³
= 8
Bài 6
a) 11³ - 1 = 11³ - 1³
= (11 - 1)(11² + 11.1 + 1²)
= 10.(121 + 11 + 1)
= 10.133
= 1330
b) Đặt B = x³ - y³ = (x - y)(x² + xy + y²)
= (x - y)(x² - 2xy + y² + 3xy)
= (x - y)[(x - y)² + 3xy]
Thay x - y = 6 và xy = 9 vào B ta được:
B = 6.(6² + 3.9)
= 6.(36 + 27)
= 6.63
= 378
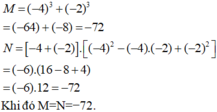
\(x^3+y^3=\left(x+y\right)\left(x^2+xy+y^2\right)\)
\(7\left(x^2+y^2+14\right)\)
\(=7\left[\left(x+y\right)^2-2xy+14\right]\)
\(=7\left(7^2-2.14+14\right)\)
\(=7\left(49-14\right)=7.35=245\)