Cho tam giác ABC có góc a bằng 110 độ, góc b bằng 35 độ, BC=3. Tính AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 7 2023
a: Xét ΔABC có AB<AC<BC
nên góc C<góc B<góc A
b: góc C=180-50-60=70 độ
Xét ΔABC có góc A<góc B<góc C
nên BC<AC<AB
DH
1
12 tháng 8 2023
góc C=180-30-80=70 độ
Xét ΔABC có
AB/sinC=AC/sinB=BC/sinA
=>3/sin70=AC/sin80=BC/sin30
=>\(BC\simeq1,6\left(cm\right);AC\simeq3,14\left(cm\right)\)
M
1
15 tháng 5 2023
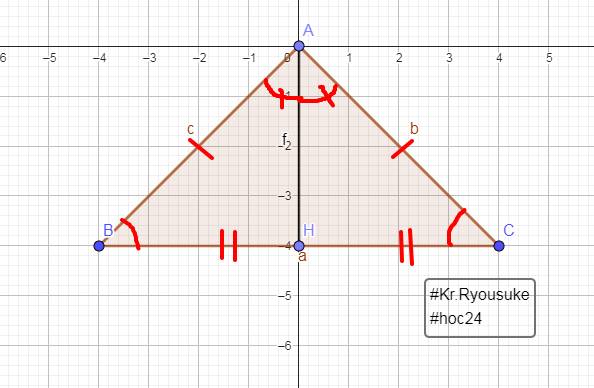
`a,`
Vì `\Delta ABC` cân tại A:
`-> \text {AB = AC, }` $\widehat {B} = \widehat {C}$.
Xét `\Delta AHB` và `\Delta AHC` :
`\text {AB = AC}`
$\widehat {B} = \widehat {C}$
$\widehat {AHB} = \widehat {AHC} (=90^0) (\text {AH là đường cao})$
`=> \Delta AHB = \Delta AHC (ch-gn)`
`b,`
Vì `\Delta AHB = \Delta AHC (a)`
`->` $\widehat {BAH} = \widehat {CAH} (\text {2 góc tương ứng})$
Mà $\widehat {BAH} = 35^0$
`->` $\widehat {BAH} = \widehat {CAH} = 35^0.$
`c,`
`\Delta AHB = \Delta AHC (a)`
`-> \text {BH = CH (2 cạnh tương ứng)}`
Mà `\text {BH = 4 cm}`
`-> \text {BH = CH = 4 cm}`
20 tháng 2 2021
a) Xét ΔBAD vuông tại A và ΔBHD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)(BD là tia phân giác của \(\widehat{ABH}\))
Do đó: ΔBAD=ΔBHD(cạnh huyền-góc nhọn)
Suy ra: BA=BH(hai cạnh tương ứng) và AD=HD(Hai cạnh tương ứng)
Ta có: BA=BH(cmt)
nên B nằm trên đường trung trực của AH(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: AD=HD(cmt)
nên D nằm trên đường trung trực của AH(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra BD là đường trung trực của AH
\(\Leftrightarrow AH\perp BD\)(đpcm)
b) Xét ΔDAH có DA=DH(cmt)
nên ΔDAH cân tại D(Định nghĩa tam giác cân)
\(\Leftrightarrow\widehat{DAH}=\dfrac{180^0-\widehat{ADH}}{2}\)(Số đo của một góc ở đáy trong ΔDAH cân tại D)
\(\Leftrightarrow\widehat{DAH}=\dfrac{180^0-110^0}{2}=35^0\)
Ta có: \(\widehat{BAH}+\widehat{DAH}=\widehat{BAD}\)(tia AH nằm giữa hai tia AD,AB)
\(\Leftrightarrow\widehat{BAH}+35^0=90^0\)
hay \(\widehat{BAH}=55^0\)
Vậy: \(\widehat{BAH}=55^0\)
QE
2
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 7 2021
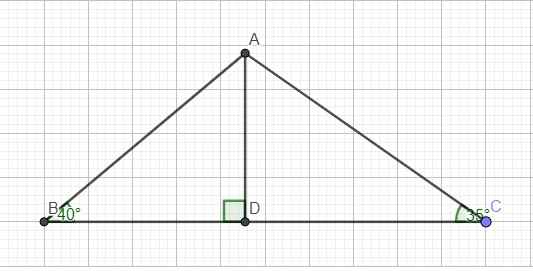
Kẻ đường cao AD ứng với BC
Trong tam giác vuông ABD:
\(cotB=\dfrac{BD}{AD}\Rightarrow BD=AD.cotB\)
Trong tam giác vuông ACD:
\(cotC=\dfrac{CD}{AD}\Rightarrow CD=AD.cotC\)
\(\Rightarrow BD+CD=AD.cotB+AD.cotC\)
\(\Rightarrow BC=AD\left(cotB+cotC\right)\)
\(\Rightarrow AD=\dfrac{BC}{cotB+cotC}\)
Trong tam giác vuông ACD:
\(sinC=\dfrac{AD}{AC}\Rightarrow AC=\dfrac{AD}{sinC}=\dfrac{BC}{sinC\left(cotB+cotC\right)}=\dfrac{20}{sin35^0\left(cot40^0+cot35^0\right)}=13,3\left(cm\right)\)
Ta có :\(\dfrac{BC}{sinA}=\dfrac{AC}{sinB}\Rightarrow AC=\dfrac{BC.sinB}{sinA}\approx2\)