Tìm phép biến hình biến đồ thị y=x2 thành đồ thị:
a/ y=x2/2
b/ y=x2/4 + 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 12 2023
b: Tọa độ đỉnh của (P): y=x2-4x+3 là:
\(\left\{{}\begin{matrix}x=\dfrac{-b}{2a}=\dfrac{-\left(-4\right)}{2}=\dfrac{4}{2}=2\\y=-\dfrac{b^2-4ac}{4a}=-\dfrac{\left(-4\right)^2-4\cdot1\cdot3}{4}=-\dfrac{16-12}{4}=-1\end{matrix}\right.\)
Bảng biến thiên:
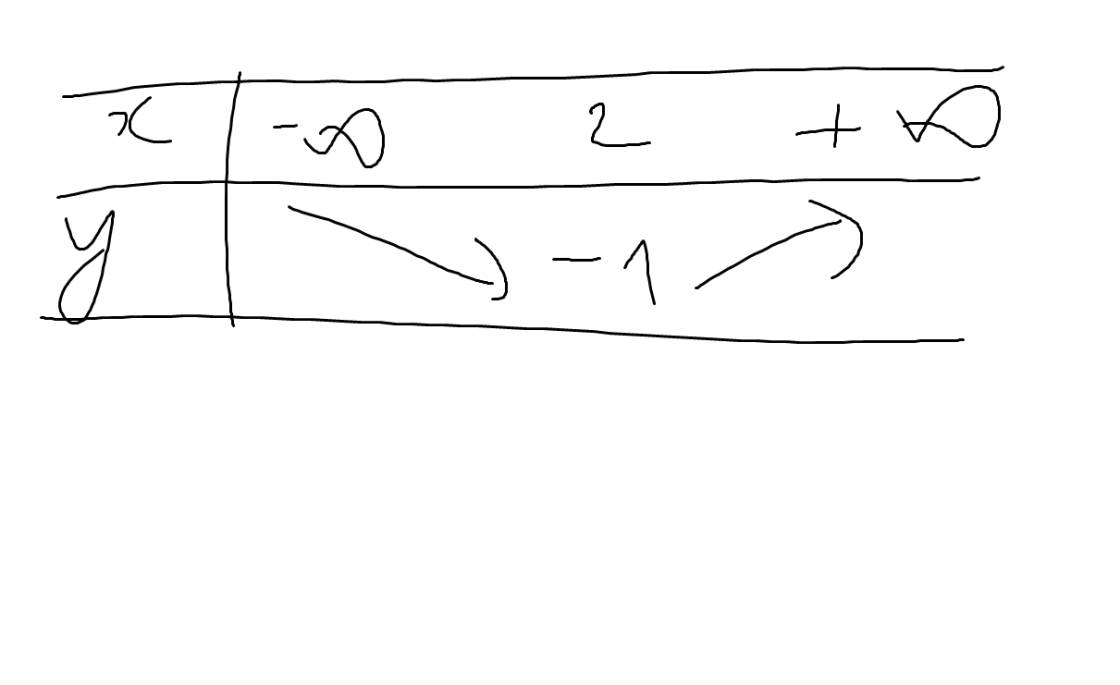
Vẽ đồ thị hàm số:
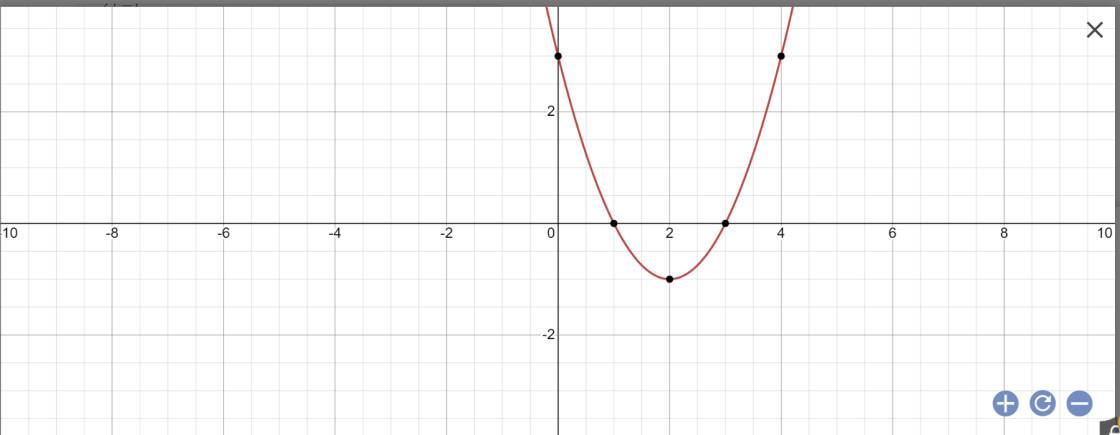
e: Tọa độ đỉnh của (P): y=-x2+4x-3 là:
\(\left\{{}\begin{matrix}x=\dfrac{-b}{2a}=\dfrac{-4}{2\cdot\left(-1\right)}=\dfrac{4}{2}=2\\y=-\dfrac{b^2-4ac}{4a}=-\dfrac{4^2-4\cdot\left(-1\right)\cdot\left(-3\right)}{4\cdot\left(-1\right)}=1\end{matrix}\right.\)
Bảng biến thiên:
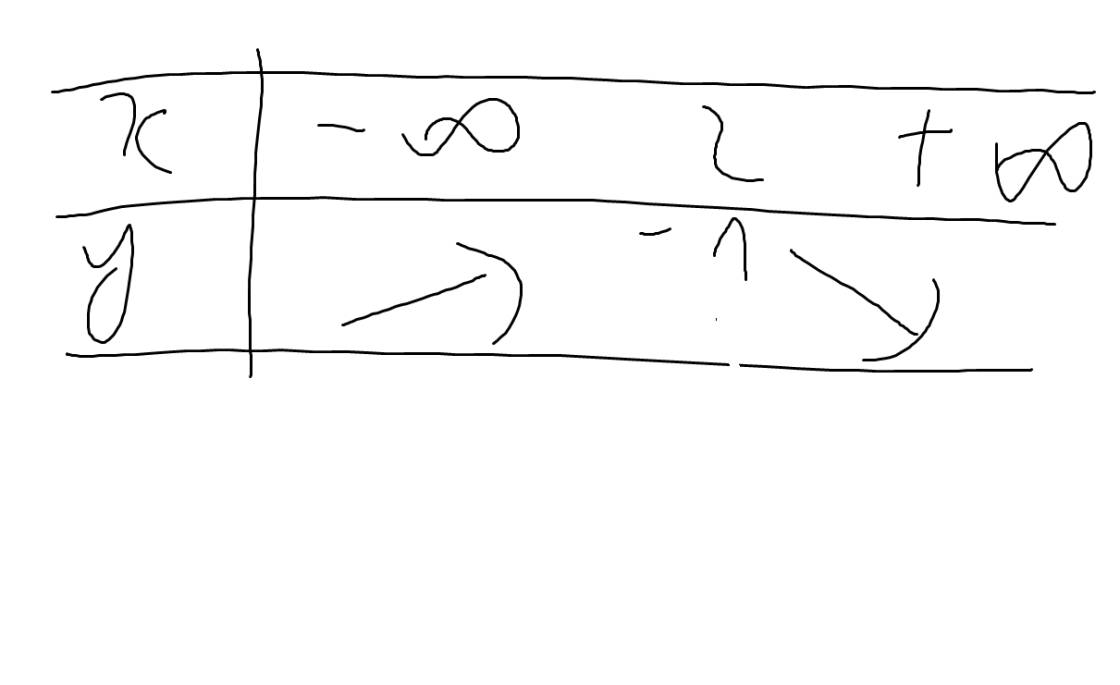
vẽ đồ thị hàm số:
CM
10 tháng 11 2018
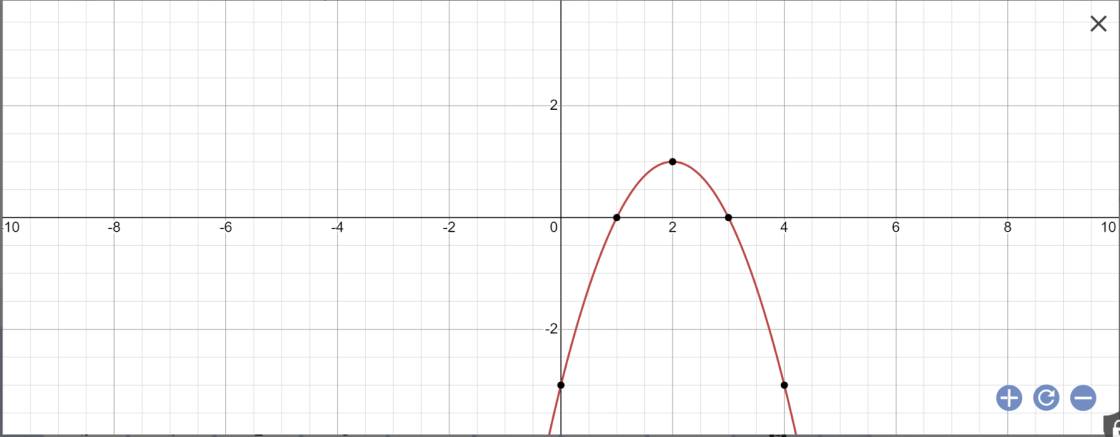
Có 
Bất phương trình này khó giải trực tiếp, do vậy ta sẽ chọn x thoả mãn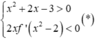 
TH1: Nếu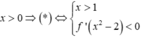 
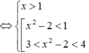
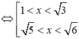
Chọn đáp án C.
TH2: Nếu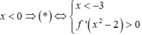 
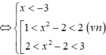
KC
0
a) từ công thức \(\left\{{}\begin{matrix}X'=X+a\\Y'=Y+b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}X=X'-a\\Y=Y'-b\end{matrix}\right.\)
ta \(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{\sqrt{2}}=x+a\\y=y+b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\left(\dfrac{-2+\sqrt{2}}{2}\right)x\\b=0\end{matrix}\right.\)
vậy phép biến hình biến đồ thị \(y=x^2\) thành \(y=\dfrac{x^2}{2}\) là \(T_{\overrightarrow{u}}\left(y=x^2\right)\)
với \(\overrightarrow{u}:\left(\left(\dfrac{-2+\sqrt{2}}{2}\right)x;0\right)\)
bạn làm tương tự cho câu b nha