phân tích đa thức thành nhân tử: 2x3y-2xy3-4xy2-2xy
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
15 tháng 6 2018
2x3y – 2xy3 – 4xy2 – 2xy
= 2xy(x2 - y2 - 2y - 1)
= 2xy[x2 - (y2 + 2y + 1)]
= 2xy[x2 - (y + 1)2 ]
= 2xy(x + y + 1)(x - y - 1)
CM
30 tháng 10 2018
2 x 3 y – 2 x y 3 – 4 x y 2 – 2 x y = 2 x y ( x 2 – y 2 – 2 y – 1 ) = 2 x y [ x 2 – ( y 2 + 2 y + 1 ) ] = 2 x y [ x 2 – ( y + 1 ) 2 ]
= 2xy(x – y – 1)(x + y + 1)
Đáp án cần chọn là: A
FH
2
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 1
\(x^4-y^4+2x^3y-2xy^3\)
\(=\left(x^2+y^2\right)\left(x^2-y^2\right)+2xy\left(x^2-y^2\right)\)
\(=\left(x^2-y^2\right)\left(x^2+y^2+2xy\right)\)
\(=\left(x-y\right)\left(x+y\right)\left(x+y\right)^2\)
\(=\left(x-y\right)\left(x+y\right)^3\)
GH
4 tháng 1
\(x^4-y^4+2x^3y-2xy^3\\ =\left(x^2\right)^2-\left(y^2\right)^2+2xy\left(x^2-y^2\right)\\ =\left(x^2-y^2\right)\left(x^2+y^2\right)+2xy\left(x^2-y^2\right)\\ =\left(x^2-y^2\right)\left(x^2+y^2+2xy\right)\\ =\left(x-y\right)\left(x+y\right)\left(x+y\right)^2\\ =\left(x-y\right)\left(x+y\right)^3\)
CM
3 tháng 3 2018
Ta có
(A):
16 x 4 ( x – y ) – x + y = 16 x 4 ( x – y ) – ( x – y ) = ( 16 x 4 – 1 ) ( x – y ) = [ ( 2 x ) 4 – 1 ] ( x – y ) = [ ( 2 x ) 2 – 1 ] [ ( 2 x ) 2 + 1 ] ( x – y ) = ( 2 x – 1 ) ( 2 x + 1 ) ( 4 x 2 + 1 ) ( x – y )
Nên (A) sai
Và (B):
2 x 3 y – 2 x y 3 – 4 x y 2 – 2 x y = 2 x y ( x 2 – y 2 – 2 y – 1 ) = 2 x y [ x 2 – ( y 2 + 2 y + 1 ) ] = 2 x y [ x 2 – ( y + 1 ) 2 ] = 2 x y ( x – y – 1 ) ( x + y + 1 ) .
Nên (B) sai.
Vậy cả (A) và (B) đều sai.
Đáp án cần chọn là: C
10 tháng 8 2021
\(-8x^2y^2-12xy^2-4xy^2=-8x^2y^2-16xy^2\)
\(=-8xy^2\left(x+2\right)\)
H
12 tháng 10 2023
`x^2 -4x+4-y^2`
`=(x^2 -4x+4)-y^2`
`=(x-2)^2 -y^2`
`=(x-2-y)(x-2+y)`
`x^2+2xy+y^2-x-y`
`=(x^2+2xy+y^2) -(x+y)`
`=(x+y)^2 -(x+y)`
`=(x+y)(x+y-1)`
`x^2-2xy+y^2-9`
`=(x^2-2xy+y^2)-3^2`
`=(x-y)^2-3^3`
`=(x-y-3)(x-y+3)`
Tách ra đi cậu.
PT
1
NH
2
KV
12 tháng 12 2023
2xy - 4x + 5y - 10
= (2xy - 4x) + (5y - 10)
= 2x(y - 2) + 5(y - 2)
= (y - 2)(2x + 5)
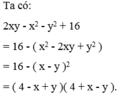
\(=2xy\left(x^2-y^2-2y-1\right)\)
\(=2xy\left[x^2-\left(y^2+2y+1\right)\right]\)
\(=2xy\left[x^2-\left(y+1\right)^2\right]\)
\(=2xy\left(x-y-1\right)\left(x+y+1\right)\)
\(2x^3y-2xy^3-4xy^2-2xy\)
\(=2xy\left(x^2-y^2-2y-1\right)\)
\(=2xy\left[x^2-\left(y+1\right)^2\right]\)
\(=2xy\left(x-y-1\right)\left(x+y+1\right)\)