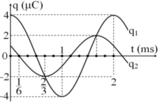
2 mạch dao động lý tưởng L1C1 và L2C2 với C1=C2=0,1microF , L1=L2=1microH . Ban đầu tích điện cho tụ C1 đến hiệu điện thế 6V và tụ C2 đến hiệu điện thế 12V rồi cho mạch dao động . Thời gian ngắn nhất kể từ khi mạch dao động bắt đầu dao động thì hiệu điện thế trên C1 và C2 chênh lệch nhau 3V
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Chu kì dao động của mạch LC: T = 2 π L C = 2 p 2.10 − 6 .0 , 2.10 − 6 = 4.10 − 6 s
Dễ thấy rằng điện thế trên hai tụ lệch nhau 4V ứng với u 1 = 1 2 U 01 = 4 V ; u 2 = 1 2 U 02 = 8 V
⇒ Δ t = T 6 = 2.10 − 6 3 s

Đáp án D
Cách giải:
Chọn gốc thời gian là lúc cả hai mạch bắt đầu dao độngPhương trình điện áp trên 2 tụ C1 và C2 lần lượt có dạng: u1= 3cosωt(V) và u2 = 9cosωt(V)
Độ chênh điện áp tức thời giữa hai tu ̣: Δu = u1 – u2 = 6cosωt (V)
Ứng với khoảng thời gian cần tìm vecto quay biểu diễn cho Δu quay được một góc π/3 nên :
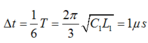



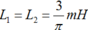
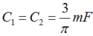
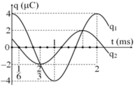


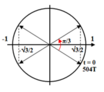
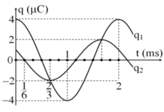


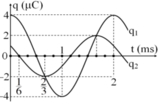


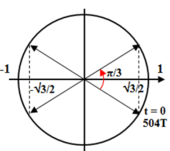


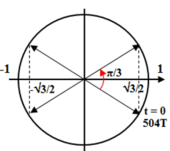
Xem t = 0 là lúc cả hai mạch bắt đầu dao động
Phương trình hiệu điện thế trên 2 tụ C1 và C2 lần lượt có dạng
\(\begin{cases}u_1=12cos\left(\omega t\right)\left(V\right)\\u_2=6cos\left(\omega t\right)\left(V\right)\end{cases}\)
Độ chênh lệch Hiệu điện thế: \(\Delta u=u_1-u_2=6cos\left(\omega t\right)\left(V\right)\)
\(u_1-u_2=6cos\left(\omega t\right)=\pm3\Rightarrow cos\left(\omega t\right)=\pm0,5\Rightarrow cos\left(\frac{2\pi}{T}t\right)=\pm0,5\)
\(\Rightarrow\Delta t_{min}=\frac{T}{6}=\frac{10^{-6}}{3}s\)
\(\frac{10^{-6}}{3}\)s