Cho G là trọng tâm của tam giác ABC;AM là đường trung tuyến,khi đó tỉ số GM/AM là bao nhiêu ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QT
1
17 tháng 9 2023
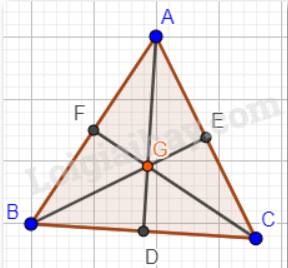
Tam giác ABC đều nên AB = AC = BC.
G là trọng tâm tam giác ABC nên AD, BE, CF là các đường trung tuyến trong tam giác.
Suy ra: AF = BF = AE = CE = BD = CD.
Xét tam giác ADB và tam giác ADC có:
AB = AC (tam giác ABC đều);
AD chung
BD = CD (D là trung điểm của đoạn thẳng BC).
Vậy \(\Delta ADB = \Delta ADC\)(c.c.c) nên \(\widehat {ADB} = \widehat {ADC}\) ( 2 góc tương ứng).
Mà ba điểm B, D, C thẳng hàng nên \(\widehat {ADB} = \widehat {ADC} = 90^\circ \)hay \(AD \bot BC\). (1)
Tương tự ta có:
\(\widehat {AEB} = \widehat {CEB} = 90^\circ \) hay\(BE \bot AC\). (2)
\(\widehat {AFC} = \widehat {BFC} = 90^\circ \) hay\(CF \bot AB\). (3)
Từ (1), (2), (3) suy ra G là giao điểm của ba đường cao AD, BE, CF.
Vậy G cũng là trực tâm của tam giác ABC.
VT
17 tháng 9 2017
ta gọi AH,AK là 2 đường trung tuyến của tam giác ABM và AMC
ta có D,G,N lần lượt là trọng tâm tam giác ABM,ABC,AM
=> \(\frac{AD}{AH}=\frac{AG}{AM}=\frac{AN}{AK}=\frac{2}{3}\) (tính chất trọng tâm)
=> DG//BC(đingj lí ta lét) và GN//BC(định lí ta lét )
=> D,G,N thẳng hàng(ĐPCM)
VT
17 tháng 9 2017
bạn ơi xem lại đề đi sao M lại là trọng tâm của tam giác AMB?
H
8 tháng 4 2022
VẼ DF VUÔNG GÓC VỚI AB, EG VUÔNG GÓC VỚI AC
BD = CE => SABC = SACE => AB.DF = AC.EG => DF/EG = AC/AB (1)
TAM GIÁC ADF ĐỒNG DẠNG VỚI TAM GIÁC AEG => DF/EG = AD/AE (2)
TỪ (1) VÀ (2) => AC/AB = AD/AE, CHO TA TAM GIÁC ABE ĐỒNG DẠNG VỚI TAM GIÁC ACD
=> GÓC ABE = GÓC ACD => TAM GIÁC ABC CÂN (đpcm)
tự vẽ hình
Vì G là trọng tâm của ABC nên
AG = 2/3AM
=> GM = AM - AG = AM - 2/3AM = 1/3AM
Vậy \(\frac{GM}{AM}=\frac{1}{3}\)
Vì G là trọng tâm của ABC nên :
AG = 2/3 AM
=> GM = AM - AG = AM - 2/3AM = 1/3 AM
Vậy GM/AM = 1/3