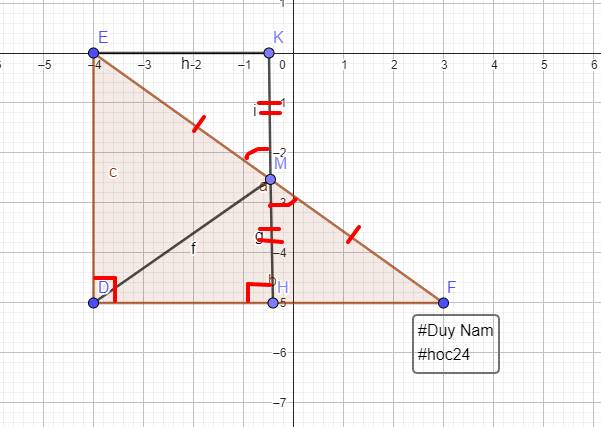
Cho tam giác DEF vuông ở D. Tia phân giác DEF cắt DF tại M. Từ M kẻ MH vuông góc với EF,MH cắt DE tại K
a)chứng minh DM=MH
b)so sánh DM và MF
c)chứng minh tam giác KEF caan
LÀM HỘ MÌNH VỚI VẼ CẢ HÌNH NỮA NHÉ NHANH LÊN CẢ BẠN ƠI GÚP MÌNH VS
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Xét 2 tam giác vuông DEM và HEM có:
ME cạnh chung
\(\widehat{DEM}\)=\(\widehat{HEM}\)(gt)
=> tam giác DEM=tam giác HEM(CH-GN)
b, vì tam giác DEM=tam giác HEM(câu a) suy ra MD=MH(2 cạnh tương ứng)
c, trong tam giác FKE có: FD,KH là 2 đường cao cắt nhau tại M
=> K,M,H thẳng hàng

Xét `\Delta MHF` và `\Delta MKE`:
`\text {MH = MK (gt)}`
$\widehat {KME} = \widehat {HMF} (\text {đối đỉnh})$
`\text {ME = MF (trung tuyến DM)}`
`=> \Delta MHF = \Delta MKE (c-g-c).`
Xét ΔMHF và ΔMKE có
MH=MK
góc HMF=góc KME
MF=ME
=>ΔMHF=ΔMKE

b. Ta co goc EMD + goc EMH =90 mà DEM = HEM nen EMD = EMH. Xet 2 tam giac DEM va HEM có EH canh chung, goc EMH =EMD, DEM=HEM
C. EF=EK suy ra tam giac EFK can tai E. EM la tia phan giác, cung là đường cao, ta lại có ED vuong góc voi EK. Suy ra M là trực tâm. Mà MH vuong goc EF. Suy ra KMH thang hang

a: Xét ΔMED vuông tại E và ΔMIN vuôngtại I có
MD=MN
góc EMD=góc IMN
=>ΔMED=ΔMIN
b: ΔMED=ΔMIN
=>góc MDE=góc MNI=góc MDP
=>DP=NP
a,Vì ΔDEM vuông tại D nên:
góc DEM+Góc EMD=90o(1)
Mặt khác,ΔEMH vuông tại H nên:
Góc HEM+góc EMH=90o(2)
mà góc DEM=góc HEM(gt) (3)
Từ 1;2;3=>góc DME=góc EMH
Xét ΔDEM và ΔHEM có:
góc DME=góc EMH(c/m trên)
EM là cạnh chung
góc DEM=góc HEM(gt)
=>ΔDEM=ΔHEM(g-c-g)
=>DM=MH(2 cạnh tương ứng)