Hai thôn nằm ở hai vị trí A,B cách nhau một con sông (Xem hai bờ sông là hai đường thẳng song song ) . Người ta dự kién xây một cây cầu bắc qua sông (MN) và làm hai đoạn thẳng AM và BN .Tìm vị trí M,N sao cho AM+BN là ngắn nhất .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


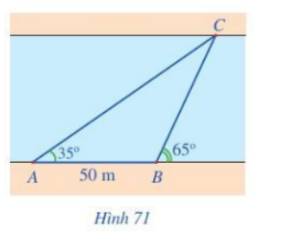
Ta có: \(\widehat C = {65^o} - {35^o} = {30^o}\)(tính chất góc ngoài)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}} \Rightarrow AC = \frac{{AB.\sin B}}{{\sin C}}\)
\( \Leftrightarrow AC = \frac{{50.\sin ({{180}^o} - {{65}^o})}}{{\sin {{30}^o}}} \approx 90,63.\)
Độ rộng của khúc sông là: \(AC.\sin A = 90,63.\sin {35^o} \approx 52\;(m)\)

Xét ΔABC có \(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0\)
=>\(\widehat{ABC}+59^0+82^0=180^0\)
=>\(\widehat{ABC}=39^0\)
Xét ΔABC có \(\dfrac{AC}{sinB}=\dfrac{AB}{sinC}\)
=>\(\dfrac{25}{sin39}=\dfrac{AB}{sin82}\)
=>\(AB=25\cdot\dfrac{sin82}{sin39}\simeq39,34\left(m\right)\)

Đáp án C
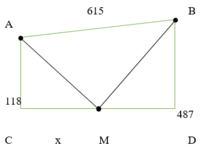
Cách 1: Giải bằng hàm số
Đặt CM = x (x > 0)
Dễ tính ra CD ![]()
Từ đề bài ta có: f (x) = ![]()
Quãng đường ngắn nhất người đó có thể đi
⇔ Giá trị nhỏ nhất của f(x) trên (0;492)
Ta có: f’(x) = 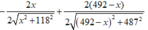
=> f’(x) = 0
![]()
![]()
![]()
![]()
![]()
Ta có bảng biến thiên
| x |
0 |
0 |
492 |
| y’ |
|
+ 0 - |
|
| y |
779,8 |
||
Vậy quãng đường ngắn nhất mà người đó có thể đi là: 779,8
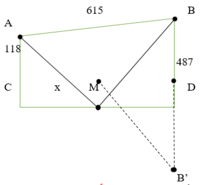
Cách 2: Giải bằng hình học
Gọi B’ là điểm đối xứng của B qua D
Dễ thấy AM + MB = AM + MB’
⇔ AM + MB ngắn nhất
⇔ AM + MB’ ngắn nhất
Dễ thấy theo bất đẳng thức tam giác: AM + MB’ ≥ AB’
⇔ AM + MB’ ngắn nhất ó AM + MB’ = AB’
Dấu “=” xảy ra khi và chỉ khi A, M, B’ thẳng hàng
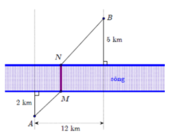

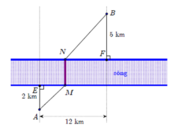

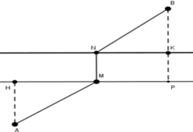

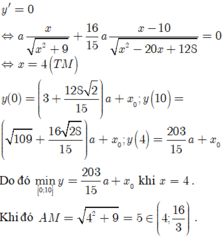

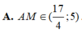
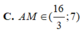


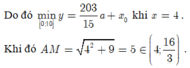

- Vì khoảng cách giữa hai bờ sống là không đổi , cho nên \(\overrightarrow{MN}=\overrightarrow{u}\).
- Tìm A’ là ảnh của A qua phép tịnh tiến theo \(\overrightarrow{u}\). Khi đó AMNA’ là hình bình hành : A’N=AM .
- Do đó : MA+NB ngắn nhất Vì : MA+NB=A’N+NB