Dùng prôtôn có động năng K1 bắn vào hạt nhân \(_4^9Be\) đứng yên gây ra phản ứng \(_1^1p + _4^9Be \rightarrow \alpha + _3^6Li\). Phản ứng này thu năng lượng bằng 2,125 MeV. Hạt nhân \(_3^6Li\) và hạt α bay ra với các động năng lần lượt bằng K2 = 4 MeV và K3 = 3,575 MeV (lấy gần đúng khối lượng các hạt nhân, tính theo đơn vị u, bằng số khối). 1 u = 931,5 MeV/c2. Góc giữa hướng chuyển động của hạt α và prôtôn bằng
A.45o.
B.90o.
C.75o.
D.120o.

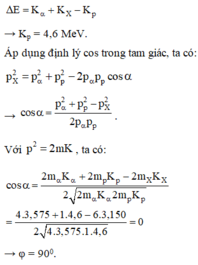
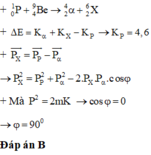
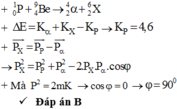
\(_1^1p + _4^9Be \rightarrow \alpha + _3^6Li\)
Phản ứng này thu năng lượng => \(W_{thu} =(m_s-m_t)c^2 = K_t-K_s\)
=> \( K_p+ K_{Be}-K_{He}- K_{Li} = W_{thu} \) (do Be đứng yên nên KBe = 0)
=> \(K_p = W_{thu}+K_{Li}+K_{He} = 2,125+4+3,575 = 9,7MeV.\)
Áp dụng định luật bảo toàn động lượng
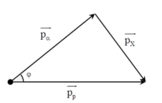
\(\overrightarrow P_{p} =\overrightarrow P_{He} + \overrightarrow P_{Li} \)
Dựa vào hình vẽ ta có
Áp dụng định lí hàm cos trong tam giác
=> \(\cos {\alpha} = \frac{P_p^2+P_{He}^2-P_{Li}^2}{2P_pP_{He}} = \frac{2.1.K_p+ 2.4.K_{He}-2.6.K_{Li}}{2.2.2m_pm_{He}K_pK_{He}} = 0.\)
Với \(P^2 = 2mK, m=A.\).
=> \(\alpha = 90^0.\)