Hạt prôtôn có động năng 2 MeV bắn phá vào hạt nhân \(_3^7Li\) đứng yên, sinh ra hai hạt nhân X có cùng động năng, theo phản ứng hạt nhân sau: \(_1^1p + _3^7 Li \rightarrow X+X\). Cho biết mp = 1,0073 u; mLi = 7,0144 u; mX = 4,0015 u. 1 u = 931 MeV/c2. Theo phản ứng trên: để tạo thành 1,5 g chất X thì phản ứng toả ra bao nhiêu năng lượng ?A.17,41...
Đọc tiếp
Hạt prôtôn có động năng 2 MeV bắn phá vào hạt nhân \(_3^7Li\) đứng yên, sinh ra hai hạt nhân X có cùng động năng, theo phản ứng hạt nhân sau: \(_1^1p + _3^7 Li \rightarrow X+X\). Cho biết mp = 1,0073 u; mLi = 7,0144 u; mX = 4,0015 u. 1 u = 931 MeV/c2. Theo phản ứng trên: để tạo thành 1,5 g chất X thì phản ứng toả ra bao nhiêu năng lượng ?
A.17,41 MeV.
B.19,65.1023 MeV.
C.39,30.1023 MeV.
D.104,8.1023 MeV.
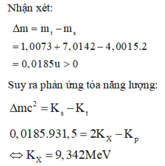
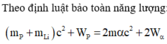
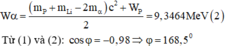
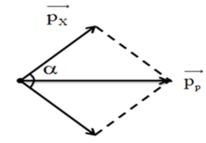
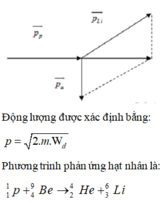
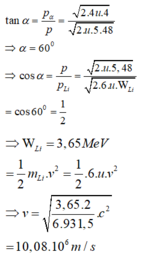
\(_1^1p + _3^7 Li \rightarrow _2^4He+_2^4He\)
\(W_{tỏa} = (m_t-m_s)c^2 =( m_{Li}+m_p - 2m_{He}).931=17,4097MeV.\)
Số hạt nhân \(_2^4He\) trong 1,5 g heli là \(N= nN_A= \frac{m}{A}.N_A = \frac{1,5}{4}.6,02.10^{23}= 2,2575.10^{23} \)(hạt)
Mỗi phản ứng tạo ra 2 hạt nhân \(_2^4He\) thì tỏa ra năng lượng là 17,4097 MeV
=> Để tạo ra 2,2572.1023 hạt nhân \(_2^4He\) thì tỏa ra năng lượng là
\(W = \frac{17,4097.2,2575.10^{23}}{2} = 1,965.10^{24}MeV.\)