1. Cho hình thang vuông MNEF vuông tại M và F, EF là đáy lớn. Hai đường chéo ME
và NF vuông góc với nhau tại O.
1) Cho biết MN = 9 cm, MF = 12 cm.
a) Giải tam giác MNF.
b) Tính độ dài các đoạn thẳng MO, FO.
c) Kẻ NH vuông góc với EF tại H. Tính diện tích tam giác FNE. Từ đó tính diện
tích tam giác FOH.
2) Chứng minh \(MF^2\)=MN.FE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: NF=15cm
Xét ΔMNF vuông tại M có sin MFN=MN/NF=3/5
nên góc MFN=37 độ
=>góc MNF=53 độ
\(MO=\dfrac{9\cdot12}{15}=\dfrac{108}{15}=7.2\left(cn\right)\)
\(FO=\dfrac{12^2}{15}=9.6\left(cm\right)\)
b: Xét ΔMFN và ΔFEM có
góc MFN=góc FEM
góc FNM=góc EMF
Do đó: ΔMFN đồng dạng với ΔFEM
Suy ra:MF/FE=MN/MF
hay \(MF^2=MN\cdot FE\)

a,i, Tính được NF=15cm; M F N ^ ≈ 37 0 và M N F ^ = 53 0
ii, Tìm được MO = 36 5 cm, FO = 48 5 cm
iii, Tìm được
S
F
N
E
=
96
c
m
2
Cách 1: Ta có S F O H S F N E = F O F N . F H F E = 9 25
=> S ∆ F O H = 34 , 56 c m 2
Cách 2: Gợi ý. Kẻ đường cao OK của ∆FOH => S ∆ F O H = 34 , 56 c m 2
b, Ta có ∆MFN ~ ∆FEM(g.g) => M F F E = M N F M <=> M F 2 = M N . F E

Hình thang MNEF vuông tại M, F có EF là đáy lớn. Hai đường chéo ME và NF vuông góc với nhau tại O
a) Cho biết MN = 9cm và MF = 12cm, Hãy giải tam giác MNF,
MN=9;MF=12; FN=√9^2+12^2)=3.√(9+16)=15
^F=actan(3/4)
^N=artan(4/3)
S=1 /2.9.12=54
hm=2S/NF=36/5
...
tính MO
MO=hm=36/5
và FO,
FO=√MF^2-MO^2)=9√(1-4^2/5^2)=27/5
kẻ NF ????? vuông góc với EF tại H.

hoicj tốtttttttttttttttttttttttttttttttttttttttttttttttt


a: NF=15cm
Xét ΔMNF vuông tại M có sin MFN=MN/NF=3/5
nên góc MFN=37 độ
=>góc MNF=53 độ
b: \(MO=\dfrac{9\cdot12}{15}=\dfrac{108}{15}=7.2\left(cn\right)\)
\(FO=\dfrac{12^2}{15}=9.6\left(cm\right)\)
c: \(S_{EOF}=\dfrac{OF\cdot OE}{2}\)
FE=12^2/9=16cm
\(OE=\dfrac{16^2}{20}=\dfrac{256}{20}=12.8\left(cm\right)\)
\(S_{EOF}=\dfrac{12.8\cdot9.6}{2}=12.8\cdot4.8=61.44\left(cm^2\right)\)

a: NF=15cm
Xét ΔMNF vuông tại M có sin MFN=MN/NF=3/5
nên góc MFN=37 độ
=>góc MNF=53 độ
b: \(MO=\dfrac{9\cdot12}{15}=\dfrac{108}{15}=7.2\left(cn\right)\)
\(FO=\dfrac{12^2}{15}=9.6\left(cm\right)\)
c: \(S_{EOF}=\dfrac{OF\cdot OE}{2}\)
FE=12^2/9=16cm
\(OE=\dfrac{16^2}{20}=\dfrac{256}{20}=12.8\left(cm\right)\)
\(S_{EOF}=\dfrac{12.8\cdot9.6}{2}=12.8\cdot4.8=61.44\left(cm^2\right)\)

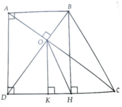
a, Tính được DB=15cm. A D B ^ ≈ 37 0 ; A B D ^ ≈ 53 0
b, Tính được AO=7,2cm, DO=9,6cm và AC=20cm
c, Kẻ OK ⊥ DC tại K
DH=AB=9cm, DC=16cm, DK=5,76cm và OK=7,68cm
Từ đó S D O H = O K . D H 2 = 7 , 68 . 9 2 = 34,56 c m 2

Câu 1: Tam giác ABC vuông tại A có AM là đường trung tuyến ứng với cạnh huyền BC
=> AM=\(\frac{1}{2}\)BC mà AM=6 cm=> BC=12cm.
Tam giác ANB vuông tại A có AN2+AB2=BN2 (Theo Pytago) mà BN=9cm (gt)
=>AN2+AB2=81 Lại có AN=\(\frac{1}{2}\)AC =>\(\frac{1}{2}\)AC2+AB2=81 (1)
Tam giác ABC vuông tại A có: AC2+AB2=BC2 => BC2 - AB2 = AC2 (2)
Từ (1) và (2) suy ra \(\frac{1}{4}\)* (BC2 - AB2)+AB2=81 mà BC=12(cmt)
=> 36 - \(\frac{1}{4}\)AB2+AB2=81
=> 36+\(\frac{3}{4}\)AB2=81
=> AB2=60=>AB=\(\sqrt{60}\)
C2
Cho hình thang cân ABCD có đáy lớn CD = 1
C4
Câu hỏi của Thiên An - Toán lớp 9 - Học toán với OnlineMath

1)
a) Áp dụng định lí Pytago vào ΔMNF vuông tại M, ta được:
\(NF^2=MF^2+MN^2\)
\(\Leftrightarrow NF^2=9^2+12^2=225\)
hay NF=15(cm)
Xét ΔMNF vuông tại M có
\(\sin\widehat{MFN}=\dfrac{MN}{NF}=\dfrac{9}{15}=\dfrac{3}{5}\)
hay \(\widehat{MFN}\simeq37^0\)
\(\Leftrightarrow\widehat{MNF}=53^0\)