Giải phương trình bằng cách đưa về hệ đối xứng

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


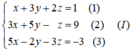
Nhân phương trình (2) với 2 rồi cộng với phương trình (1) và nhân phương trình (2) với 3 rồi trừ đi phương trình (3), phương trình (2) giữ nguyên ta được:
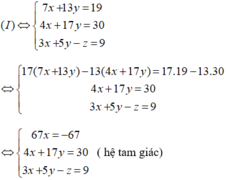
Giải hệ phương trình trên ta được x = -1; y = 2; z = -2.
Vậy hệ phương trình có nghiệm (x; y; z) = (-1; 2; -2)

2x3 + 5x2 – 3x = 0
⇔ x(2x2 + 5x – 3) = 0
⇔ x.(2x2 + 6x – x – 3) = 0
⇔ x. [2x(x + 3) – (x + 3)] = 0
⇔ x.(2x – 1)(x + 3) = 0
⇔ x = 0 hoặc 2x – 1 = 0 hoặc x + 3 = 0
+ 2x – 1 = 0 ⇔ 2x = 1 ⇔ x = 1/2.
+ x + 3 = 0 ⇔ x = -3.
Vậy phương trình có tập nghiệm 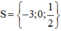

x3 + 3x2 – 2x – 6 = 0
⇔ (x3 + 3x2) – (2x + 6) = 0
⇔ x2(x + 3) – 2(x + 3) = 0
⇔ (x2 – 2)(x + 3) = 0
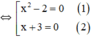
+ Giải (1): x2 – 2 = 0 ⇔ x2 = 2 ⇔ x = √2 hoặc x = -√2.
+ Giải (2): x + 3 = 0 ⇔ x = -3.
Vậy phương trình có tập nghiệm S = {-3; -√2; √2}

x3 + 3x2 + 2x = 0 ⇔ x(x2 + 3x + 2) = 0
⇔ x = 0 hoặc x2 + 3x + 2 = 0 (1)
Giải phương trình (1) ta được các nghiệm x = -1; x = -2
Vậy phương trình đã cho có 3 nghiệm x = 0; x = -1; x = -2

x 3 + 3 x 2 + 2 x = 0 ⇔ x ( x 2 + 3 x + 2 ) = 0
⇔ x = 0 hoặc x 2 + 3 x + 2 = 0 ( 1 )
Giải phương trình (1) ta được các nghiệm x = -1; x = -2
Vậy phương trình đã cho có 3 nghiệm x = 0; x = -1; x = -2

\(sinx=\dfrac{2tan\dfrac{x}{2}}{tan^2\dfrac{x}{2}+1}\)
\(cosx=\dfrac{1-tan^2\dfrac{x}{2}}{1+tan^2\dfrac{x}{2}}\)
Đặt \(t=tan\dfrac{x}{2}\)
Khi đó pt: \(\Rightarrow a\cdot\dfrac{2t}{t^2+1}+b\cdot\dfrac{1-t^2}{1+t^2}=c\)
\(\Rightarrow2t\cdot a+\left(1-t^2\right)\cdot b=\left(1+t^2\right)\cdot c\)