Cho \(2cm^3\) nước vào trong một ống nhỏ giọt nước có đường kính miệng \(d=0,4mm\) , người ta nhỏ được tất cả \(200\) giọt. Tính hệ số căng bề mặt của nước. Lấy \(g=9,8m\text{/}s^2\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khối lượng mỗi giọt nước: m = 0 , 95.10 − 3 20 = 4 , 75.10 − 5 k g
Ta có : P = m.g = 4,75.10-4N
Mà P= Fc ⇒ σ = F c π . d = 7,56.10-2 ( N/m )

Khi giọt nước bắt đầu rơi ta coi trọng lượng giọt nước đúng bằng lực căng mặt ngoài tác dụng lên vòng tròn trong của ống.
Vậy ta có: P = F0 ⇒ m g = π d σ ⇒ σ = m g π d
Khối lượng một giọt nước là m = 1 , 9 40 = 0 , 0475 g = 0 , 0475.10 − 3 k g
⇒ σ = 0 , 0475.10 − 3 .10 3 , 14.2.10 − 3 = 0 , 475 6 , 28 = 0 , 0756 N / m

Lực căng bề mặt của nước kéo giọt lên : \(F=\sigma l=\sigma\pi d\)
với \(l=\pi d\) là chu vi vòng thắt của giọt nước.
Trọng lượng của giọt nước \(p=\frac{mg}{40}\)
Giọt nước rơi xuống :
\(p\ge F\Leftrightarrow\ge\sigma\pi d\Rightarrow\sigma\le\frac{mg}{40\pi d}=0,0756\left(N\text{/}m\right)\)

Đổi đơn vị:
t = 65 phút = 65.60 = 3900s
M = 100g = 0,1kg
d = 4mm = 4.10−3m
Nhận xét: Rượu chảy ra khi lực căng bề mặt bằng trọng lực của một giọt rượu
→ P1 = F ↔ mg = σl
Ta có:
Thời gian giọt này rơi sau giọt kia là 2s và sau 65 phút có 100g rượu chảy ra => khối lượng của một giọt rượu: m = M t 2
độ dài đường giới hạn chất lỏng chính bằng chu vi của ống: l = πd
Từ đó, ta suy ra:
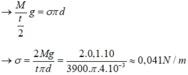
Đáp án: A

Trọng lượng P của mỗi giọt rượu khi bắt đầu rơi khỏi miệng ống nhỏ giọt có độ lớn bằng lực căng bề mặt F c của rượu tác dụng lên chu vi của miệng ống nhỏ giọt, tức là :
P = F c = σ l = σ π d
với σ là hệ số căng bề mặt của rượu và l = π d là chu vi của miệng ống nhỏ giọt.
Gọi M là khối lượng rượu chảy khỏi miệng ống trong thời gian t. Vì hai giọt rượu kế tiếp chảy khỏi miệng ống cách nhau 2,0 s nên trọng lượng P mỗi giọt tính bằng :
P = Mg/(t/2) = 2Mg/t
Từ đó ta tìm được :
![]()

Đổi đơn vị: V = 3 c m 3 = 3 . 10 - 6 m 3 ; d = 10 - 3 m ; ρ = 1000 k g / m 3
Ta có:
+ Khối lượng của một giọt nước: m = V . ρ 120
+ Nước chảy ra khi lực căng bề mặt bằng với trọng lực của một giọt nước: m g = σ π d
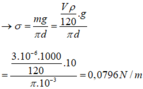
Đáp án: B

Đáp án C
Chiều dài đường giới hạn (đường tròn) :l=d.r
Lực căng mặt ngoài tác dụng lên đường giới hạn hướng thẳng đứng lên trên:
![]()
Điều kiện cân bằng: F=P
![]()
![]() N/m
N/m
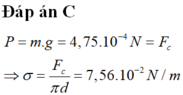
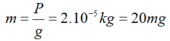
Quan sát và phân tích hiện tượng nước chảy ở ống nhỏ giọt ta thấy: đầu tiên giọt nước to dần nhưng chưa rơi xuống, đó là vì có các lực căng bề mặt tác dụng lên đường biên \(BB'\) của giọt nước, các lực này có xu hướng kéo co mặt ngoài của giọt nước lại, vì thế hợp lực của chúng hướng lên trên và có độ lớn \(\text{F=σl}\), với \(\text{l=πd}\),( \(d\) là đường kính miệng).
Đúng lúc giọt nước tách ra và rơi xuống thì trọng lượng \(P\) của giọt nước bằng lực căng bề mặt \(F\);
\(F=P\),
suy ra :
\(\text{σπd=mg}\) hay \(\sigma=\frac{mg}{\pi d}\left(1\right)\)
với \(m\) là khối lượng của \(1\) giọt nước. Theo đề bài \(2cm^3\) chứa \(200\) giọt nước, khối lượng \(2cm^3\) bằng \(2g\); vì vậy khối lượng của một giọt nước bằng
\(m=\frac{2g}{200}=0,01g=10^{-5}kg\)
Thay số vào (1) ta được: \(\sigma=\frac{9,8.10^{-5}}{3,14.0,4.10^{-3}}\approx0,078N\text{/}m\)
Hệ số căng bề mặt của nước bằng \(0,078N\text{/}m\)
mk chưa học vật lí