Cho hàm số Khi đó
=
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án C
y ' = e x . 1 2 x ⇒ y ' ' = 1 2 e x . 1 2 x . 1 x − e x . 1 2 x x = e x 4 x 1 − 1 x

Đáp án A
Ta có y ' = − 1 x 2 = − 1 1 . 1 ! x 2 ; y ' ' = − 2 x 3 = − 1 2 . 2 ! x 3 ; y ' ' ' = − 6 x 4 = − 1 3 . 3 ! x 4 .
Dự đoán y n = − 1 n . n ! x n + 1 * . Chứng minh mệnh đề (*):
* Với n=1 thì * ⇔ y ' = − 1 x 2 . Khi đó (*) đúng.
* Giả sử (*) đúng với n = k , k ≥ 1 , tức là y k = − 1 k . k ! x k + 1 .
Khi đó y k + 1 = y k ' = − 1 k . k ! x k + 1 = − 1 k . − k + 1 . k ! . x k x k + 1 2 = − 1 k + 1 . k + 1 ! x k + 2 . Vậy mệnh đề (*) cũng đúng với n=k+1 nên nó đúng với mọi n.

Đáp án B
lim x → 0 f ( x ) - f ( 0 ) x - 0 = lim x → 0 3 - 4 - x 4 - 1 4 x = lim x → 0 2 - 4 - x 4 x
= lim x → 0 ( 2 - 4 - x ) ( 2 + 4 - x ) 4 x ( 2 + 4 - x ) = lim x → 0 x 4 x 2 + 4 - x lim x → 0 1 4 ( 2 + 4 − x ) = 1 16

Đáp án A
Ta có F x = ∫ 2 e x + t anx d x = 2 e x − ln cos x + C
Mà
F 0 = 2 ⇒ C + 2 = 2 ⇒ C = 0 ⇒ F x = 2 e x − ln cos x .

Đáp án B
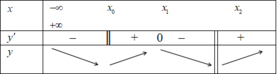
Ta có y ' = 5 2 − x 2 > 0 , ∀ x ∈ D ⇒ Hàm số đồng biến trên các khoảng − ∞ ; 2 và 2 ; + ∞


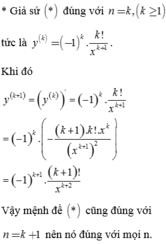


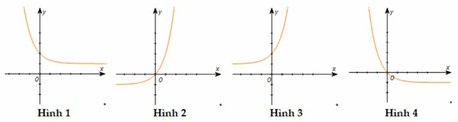

vì x =2 > 0
=> f(2) = 2 +1 =3