Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
+ Khoảng cách giữa nút và bụng gần nhất là
Δ
d
=
λ
4
=
18
cm →
λ
=
72
cm.
Ta có A M = λ 6 = 12 cm → M sẽ dao động với biên độ a M = 3 2 a B → v M m a x = 3 2 v B m a x .
→ Thời gian trong một chu kì, tốc độ của phần tử B nhỏ hơn vận tốc cực đại của M là 0,1 s tương ứng với Δ t = 2 T 3 = 0 , 1 s → T = 0 , 15 s → vận tốc truyền sóng v = λ T = 4 , 8 m/s
Đáp án D
Khoảng cách giữa một bụng và một nút liên tiếp: 
Khoảng cách từ M đến A: AM = AB - MB = 18 - 12 = 6 cm
Biên độ tại M: 
(A là biên độ của bụng sóng)
Vận tốc cực đại của phần tử tại M: 
Vận tốc cực đại của phần tử tại B (bụng sóng): 
Theo đề bài: Khoảng thời gian mà độ lớn vận tốc dao động của phần tử B nhỏ hơn vận tốc cực đại của phần tử M là 0,1 s nên:
Tốc độ truyền sóng trên sợi dây:
Đáp án D
Khoảng cách giữa một bụng và một nút liên tiếp:
Khoảng cách từ M đến A:
Biên độ tại M:
(A là biên độ của bụng sóng)
Vận tốc cực đại của phần tử tại M:
Vận tốc cực đại của phần tử tại B (bụng sóng):
Theo đề bài: Khoảng thời gian mà độ lớn vận tốc dao động của phần tử B nhỏ hơn vận tốc
Tốc độ truyền sóng trên sợi dây
Chọn đáp án D
Vì A là nút gần bụng B nhất nên A B = λ 4 = 18 ⇒ λ = 72 c m
Ta có: A M = 18 − 12 = 6 m = λ 12
⇒ A M = A b u n g 2 ⇒ v M − m a x = ω A M = ω A b u n g 2
Thời gian để v B ≤ v M − m a x ⇔ − ω A b u n g 2 ≤ v B ≤ ω A b u n g 2
⇒ Δ t = 4. T 12 = T 3 = 0 , 1 ⇒ T = 0 , 3 s ⇒ v = λ T = 240 c m / s = 2 , 4 m / s
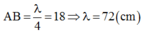
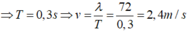
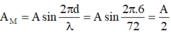
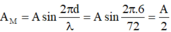
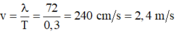
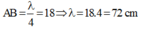
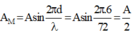
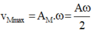
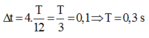
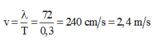
Gọi biên độ của bụng sóng là: A
Bước sóng: \(\lambda=4.AB=4.18=72cm\)
M cách A là: AM = 18 - 12 = 6cm (hoặc lấy 18 + 12 = 30 cm vẫn được, hai trường hợp như nhau)
Biên độ của M được tính theo công thức: \(A_M=A\sin\frac{2\pi d}{\lambda}=A\sin\frac{2\pi.6}{72}=\frac{A}{2}\)
\(v_{Mmax}=\omega.A_M=\frac{\omega A}{2}=\frac{v_{Bmax}}{2}\)
Ta có
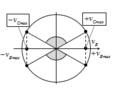
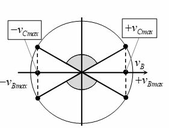
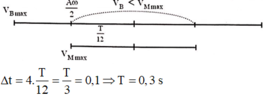
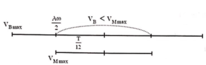
Thời gian để độ lớn vận tốc của B nhỏ hơn vận tốc cực đại của M là: \(\frac{4.30}{360}T=\frac{T}{3}=0,1\)
\(\Rightarrow T=0,3s\)
Tốc độ truyền sóng: \(v=\frac{\lambda}{T}=\frac{72}{0,3}=240\)cm/s = 2,4m/s
Chọn D.
B cách M 12cm ==> M cách A 6cm và
=Abung/2 "aM=Abung.sin(2\pi.MA/\lambda)=Abung/2")
Biên độ M:
==> vận tốc cực đại tại M :
vận tốc cực đại tại B:
Dùng vecto quay ta tính được :