Một con lắc lò xo có độ cứng k= 100 N/m, m=100g dao dông trên mặt phẳng ngang hệ số ma sát giữa vật với mặt ngẳng ngang là 0.05. Lấy g=10 m/s2. Ttừ vị trí lò xo không biến dạng kéo vật đến vị tri lò xo dãn 5cm rồi thả nhẹ cho vật dao động. Tốc độ của vật khi đi đươc 12 cm kể từ lúc thả là?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
18 tháng 1 2017
Hướng dẫn: Chọn đáp án D
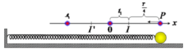
Khoảng cách:
Thời gian ngắn nhất vật đi từ P đến điểm O là
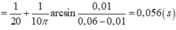
Tốc độ trung bình trong khoảng thời gian đó:
VT
21 tháng 10 2017
Đáp án B
+ Biên độ dao động bị giảm 1 lượng là
Suy ra biên độ dao động mới là:
+ Góc quét từ vị trí biên tới vị trí cân bằng mới là
VT
21 tháng 8 2019
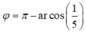
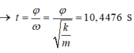
Đáp án C
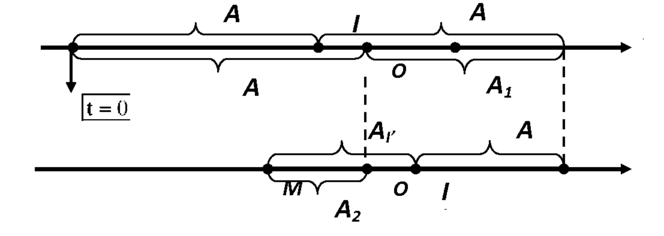
Biên độ còn lại sau mỗi lần qua VTCB O: A 1 = A - 2 x o = 5 - 2 . 1 = 3 c m
*Khi lò xo không biến dạng lần thứ 2 tức là vật đi từ chỗ bị nén ra đến vị trí lò xo giãn nhiều nhất rồi đến vị trí lò xo không biến dạng.
Áp dụng định luật bảo toàn và chuyển hóa cơ năng ta có
VT
16 tháng 7 2019
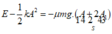
Đáp án D
Độ biến dạng của lò xo tại vị trí cân bằng tạm
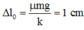
Khi vật đến vị trí lò xo không biến đạng lần 2, quãng đường tương ứng mà vật đã đi được là:
S = 2.4 + 2 = 10cm
Cơ năng lúc này của con lắc bằng hiệu thế năng ban đầu và công của lực ma sát
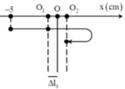
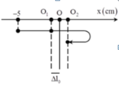
Vị trí cân bằng mới cách VTCB cũ là: \(\frac{\mu mg}{k}=\frac{0,05.0,1.10}{100}=0,05.10^{-2}m=0,05cm\)
Sau nửa chu kỳ biên độ giảm: 2. 0,05 = 0,1cm
Vật đi từ biên phải sang biên trái sẽ đi đc quãng đường là: 5 + 4,9 = 9,9cm.
Như vậy, vật cần đi tiếp: 12 - 9,9 = 2,1 cm
Khi đó, vật cách VTCB mới là: 4,9 - 2,1 - 0,05 = 2,75cm.
Biên độ mới là: A' = 4,9 - 0,05 = 4,85 cm.
Áp dụng CT độc lập, ta có tốc độ của vật là: \(v=\omega\sqrt{A^2-x^2}=10\pi\sqrt{4,85^2-2,75^2}=125,5\)(cm/s)
P/S: Đề bài này hơi lẻ, bạn xem lại giả thiết xem độ cứng lò xo và hệ số ma sát có chính xác như đề bài cho không?
trong dáp án đâu có kết quả này