tính giới hạn sau:
\(y=\frac{e^x-e^{-x}}{e^x+e^{-x}}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Với x bất kì và \(h = x - {x_0}\), ta có:
\(\begin{array}{l}f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {{x_0} + h} \right) - f\left( {{x_0}} \right)}}{h} = \mathop {\lim }\limits_{h \to 0} \frac{{{e^{{x_0} + h}} - {e^{{x_0}}}}}{h}\\ = \mathop {\lim }\limits_{h \to 0} \frac{{{e^{{x_o}}}\left( {{e^h} - 1} \right)}}{h} = \mathop {\lim }\limits_{h \to 0} {e^{{x_0}}}.\mathop {\lim }\limits_{h \to 0} \frac{{{e^h} - 1}}{h} = {e^{{x_0}}}\end{array}\)
Vậy hàm số \(y = {e^x}\) có đạo hàm là hàm số \(y' = {e^x}\)
b) Ta có \({a^x} = {e^{x\ln a}}\,\)nên \(\left( {{a^x}} \right)' = \left( {{e^{x\ln a}}} \right)' = \left( {x\ln a} \right)'.{e^{x\ln a}} = {e^{x\ln a}}\ln a = {a^x}\ln a\)

\(L=\lim\limits_{x\rightarrow0}\frac{e^x-e^{-x}}{\sin x}=\lim\limits_{x\rightarrow0}\frac{e^x-\frac{1}{e^x}}{\sin x}=\lim\limits_{x\rightarrow0}\frac{e^{2x}-1}{e^x\sin x}=\lim\limits_{x\rightarrow0}\frac{e^{2x}-1}{2x.\frac{\sin x}{2x}.e^x}\)
\(=\lim\limits_{x\rightarrow0}\frac{e^{2x}-1}{2x}.\frac{1}{\frac{\sin x}{x}}.\frac{2}{e^x}=1.\frac{1}{1}.\frac{2}{1}=2\)

Đặt \(t=x-e\Rightarrow\begin{cases}x=t+e\\x\rightarrow e;t\rightarrow0\end{cases}\)
\(\Rightarrow L=\lim\limits_{t\rightarrow0}\frac{\ln\left(t+e\right)-\ln e}{t}=\lim\limits_{t\rightarrow0}\frac{\ln\left(\frac{t+e}{e}\right)}{t}=\lim\limits_{t\rightarrow0}\left[\frac{\ln\left(1+\frac{t}{e}\right)}{\frac{t}{e}}\right]=\frac{1}{e}\)

Chọn D.
Hoành độ giao điểm của hai đường là nghiệm của phương trình (e+1)x = ( 1 + e x ) x <=> x = 0 hoặc x =1
Diện tích cần tính là S = ∫ 0 1 x e x d x - ∫ 0 1 e x d x = ∫ 0 1 x d ( e x ) - e ∫ 0 1 x d x
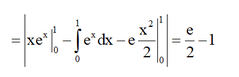
tính đạo hàm của y ạ.ko phải tính giới hạn đâu a
ta có
\(y=\frac{\left(e^x+e^{-x}\right)\left(e^x+e^{-x}\right)-\left(e^x-e^{-x}\right)\left(e^x-e^{-x}\right)}{\left(e^x+e^{-x}\right)^2}=\frac{\left(e^x+e^{-x}\right)^2-\left(e^x-e^{-x}\right)^2}{\left(e^x+e^x\right)^2}=\frac{\left(e^x+e^{-x}+e^x-e^{-x}\right)\left(e^x+e^{-x}-e^x+e^{-x}\right)}{\left(e^x+e^{-x}\right)^2}=2\frac{e^x-e^{-x}}{\left(e^x+e^{-x}\right)^2}=\frac{2}{e^x+e^{-x}}\)