một vật nhỏ thực hiện đồng thời hai dao động điều hòa cùng phương cùng tần số x1=2sin(2pit + pi/6)cm và x2=A2cos (2pit + phi 2)cm. t đo bằng dây. biết rằng tại thời điểm t= 1/6 s, vật nhỏ có li độ bằng 1/2 biên độ và bằng 1cm, đang chuyển động theo chiều âm. vậyA.A2=2cm; phi 2=pi/3 B. A2=1cm; phi2= pi/3 C.A2=1cm; phi2=-pi/3 D.A2=2cm;...
Đọc tiếp
một vật nhỏ thực hiện đồng thời hai dao động điều hòa cùng phương cùng tần số x1=2sin(2pit + pi/6)cm và x2=A2cos (2pit + phi 2)cm. t đo bằng dây. biết rằng tại thời điểm t= 1/6 s, vật nhỏ có li độ bằng 1/2 biên độ và bằng 1cm, đang chuyển động theo chiều âm. vậy
A.A2=2cm; phi 2=pi/3 B. A2=1cm; phi2= pi/3 C.A2=1cm; phi2=-pi/3 D.A2=2cm; phi2=-pi/3
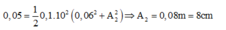
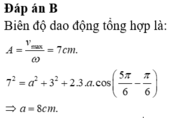
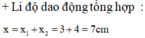
Vật thực hiện 2 dao động
\(x_1 = 2 \sin (2\pi t + \frac{\pi}{6}) = 2 \cos (2\pi t + \frac{\pi}{6} - \frac{\pi}{2}) = 2 \cos (2\pi t - \frac{\pi}{3})cm.\)
\(x_2 = A_2\cos (2\pi t + \varphi_2)cm\)
Như vậy vật coi như dao động với dao động tổng hợp là: \(x = A \cos (2\pi t + \varphi)\)
Tại thời điểm \(t = \frac{t}{6}s ; x = \frac{A}{2} = 1cm => A = 2cm.\) :
\(\frac{A}{2} = A \cos (2 \pi .\frac{t}{6} + \varphi)\)
=> \(\cos (\frac{\pi}{3}+ \varphi) = \frac{1}{2}\)
=> \(\frac{\pi}{3} + \varphi = \frac{\pi}{3} => \varphi = 0. \)
hoặc \(\frac{\pi}{3} + \varphi =- \frac{\pi}{3} = > \varphi = \frac{-2\pi}{3}\)
Mà vật chuyển động theo chiểu âm tức là \(v = x' = -A\omega \sin (\frac{\pi}{3} + \varphi) <0\)
=> \(\sin (\omega t + \varphi ) > 0 => \) Chọn \(\varphi = 0.\)
Dựng giản đồ véc tơ
\(\triangle OA_1A\) đều vì \(A= A_1 = 2cm; OA_1A = 60^0\)
=> \(A_2 = A= A_1 = 2cm; \varphi_2 = OAA_1 = \frac{\pi}{3}.\)
Chọn đáp án.A