Câu 15
a) Hãy xây dựng phương trình schrodinger cho nguyên tử He ở trạng thái dừng
b) Giải phương trình đó, với giả thiết năng lượng đẩy giữa 2 electron bị bỏ qua.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Theo phương pháp MO-Huckel. Ta dễ dàng xđ đc định thức thế kỷ:
D = \(\begin{matrix}x&1&0&0\\1&x&1&0\\0&1&x&1\\0&0&1&x\end{matrix}\)=> hệ phương trình thế kỷ : \(\begin{cases}xC_1+C_2=0\\C_1+xC_2+C_3=0\\C_2+xC_3+C_4=0\\C_3+xC_4=0\end{cases}\)
b. D = 0 \(\Leftrightarrow\)D= x4-3x2+1 = 0 \(\Leftrightarrow\begin{cases}x_1=-1,618\\x_2=-0,618\\x_3=0,618\\x_4=1,618\end{cases}\)
Thay các giá trị x1,x2,x3,x4 vào biểu thức tính năng lượng \(E=\alpha-x\beta\) ta sẽ thu đc 4 mức năng lượng electron \(\pi\).
\(\begin{cases}E_1=\alpha+1,618\beta\\E_2=\alpha+0,618\beta\\E_3=\alpha-0,618\beta\\E_4=\alpha-1,618\beta\end{cases}\)
ta có \(\psi=c_1\phi_1+c_2\phi_2+c_3\phi_3+c_4\phi_4\)
để xác định các hàm \(\psi\) ta phải tìm các hệ số ci trong biểu thức.
thay x1= -1,618 vào hệ phương trình thế kỷ ta được : \(\begin{cases}c_2=1,618c_1\\c_1+c_3=1,618c_2\\c_2+c_4=1,618c_3\\c_3=1,618c_4\end{cases}\)\(\Rightarrow\begin{cases}c_1=c_4\\c_2=c_3\end{cases}\)
kết hợp với điều kiện chuẩn hóa c12+c22+c32+c42=1 ta đc: c1=c4=0,372 và c2=c3=0,602
vậy khi x1= -1,618 ta có hàm MO tương ứng là: \(\psi_1=0.372\phi_1+0.602\phi_2+0.602\phi_3+0.372\phi_4\)
Làm tương tự với x2,x3,x4 ta sẽ thu đc \(\psi_2,\psi_3,\psi_4\)
Vậy 4 MO là : \(\begin{cases}\psi_1=0.372\phi_1+0.602\phi_2+0.602\phi_3+0.372\phi_4\\\psi_2=0.602\phi_1+0.372\phi_2-0.372\phi_3-0.602\phi_4\\\psi_3=0.602\phi_1-0.372\phi_2-0.372\phi_3+0.602\phi_4\\\psi_4=0.372\phi_1-0.602\phi_2+0.602\phi_3-0.372\phi_4\end{cases}\)

câu trả lời quá mờ không nhìn thấy được, bạn nên ghi rõ câu trả lời hoặc gõ trực tiếp vào website.

Đáp án: D
Năng lượng trạng thái dừng gồm động năng của electron và thế năng của tương tác Cu-lông:
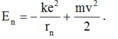
Do lực Cu-lông là lực hướng tâm nên:
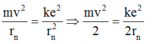
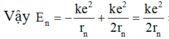
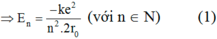

+ Áp dụng tiên đề Bo về hấp thụ và bức xạ năng lượng, ta có
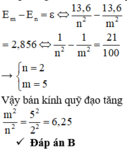
He là nguyên tử nhiều electron vì vậy ngoài tương tác của electron với hạt nhân còn có tương tác giữa các electron với nhau. Làm cho e bây giờ chuyển động trong trường không đối xứng cầu như xét ở nguyên tử hidro, việc giải phương trình Schrodinger với nhiều biến số không thể chính xác nên ta sẽ giải phương trình với mô hình gần đúng, mô hình hệ n electron độc lập. Trước tiên ta đi xây dựng phương trình Schrodinger cho nguyên tử He để thấy việc giải quyết trực tiếp nó là khó khăn
a) Xét toàn hệ He gồm 1 hạt nhân và 2 electron,
Phương trình Schrodinger có dạng: \(\widehat{H}\Psi=E\Psi\) trong đó:
\(\widehat{H}=\widehat{T}+U\) là toán tử năng lượng toàn phần với
+) \(\widehat{T}=\sum\limits^2_{i=1}-\frac{h^2}{8\pi^2m_e}\left(\frac{\partial^2}{\partial x^2_i}+\frac{\partial^2}{\partial y^2_i}+\frac{\partial^2}{\partial z^2_i}\right)\) là toán tử động năng
+) U là thế năng của hệ bao gồm \(\begin{cases}u_{1a}=-\frac{2e^2}{r_{1a}}\\u_{2a}=-\frac{2e^2}{r_{2a}}\\u_{12}=\frac{e^2}{r_{12}}\end{cases}\) , \(u_{1a},u_{2a},u_{12}\) lần lượt là thế năng hút giữa hạt nhân a và electron 1, thế năng hút giữa hạt nhân a và electrong 2, thế năng đẩy của 2 electron với nhau
\(r_{1a},r_{2a}\) lần lượt là khoảng cách giữa hạt nhân a với electron 1 và electron 2, \(r_{12}\) khoảng cách giữa 2 elecron với nhau.
\(\Psi\) là hàm sóng toàn phần của hệ phụ thuộc vào bán kính vecto của tất cả các electron trong hệ với He là \(\Psi\left(\vec{r_1},\vec{r_2}\right)\)
Vậy sau khi thay vào ta được phương trình Schrodinger của nguyên tử He như sau:
\(\left[-\frac{h^2}{8\pi^2m_e}\left(\frac{\partial^2}{\partial x_1}+\frac{\partial^2}{\partial y_1}+\frac{\partial^2}{\partial z_1}+\frac{\partial^2}{\partial x_2}+\frac{\partial^2}{\partial y_2}+\frac{\partial^2}{\partial z_2}\right)+\left(-\frac{2e^2}{r_{1a}}-\frac{2e^2}{r_{2a}}+\frac{e^2}{r_{12}}\right)\right]\Psi=E\Psi\)
b, Việc bây giờ là ta đi giải phương trình đã thành lập ở câu a để tìm biểu thức năng lượng E và hàm sóng \(\Psi\)
ta có thể thấy đây là phương trình vi phân cấp 2 rất khó giải quyết vì vậy ta phải giả thiết rằng 2 e chuyển động độc lập trong trường thế tạo bởi hạt nhân, và vì vậy trường thế này là trường đối xứng cầu.Ta bỏ qua thế tương tác giữa 2 e là \(u_{12}\) .Do đó có thế viết:
\(\widehat{H}=\widehat{H_1}+\widehat{H_2}\)
\(E=E_1+E_2\)
Mỗi e chuyển động trong hệ như vậy ứng với một phương trình Schrodinger
\(\widehat{H}_i\psi_i\left(\vec{r_i}\right)=E_i\psi_i\left(\vec{r_i}\right)\) với \(\widehat{H_i}=-\frac{h^2}{8\pi^2m_e}\left(\frac{\partial}{\partial x_i}+\frac{\partial}{\partial y_i}+\frac{\partial}{\partial z_i}\right)-\frac{2e^2}{r_{ia}}\), i=1,2 hàm sóng \(\psi_i\left(\vec{r_i}\right)\) mô tả trạng thái mỗi electron độc lập i trong nguyên tử.
Vậy việc giải các phương trình này tương tự giống phương trình Schrodinger cho nguyên tử hệ 1 e mà ta đã biết.
Và ta có năng lượng của e ở quỹ đạo n trong nguyên tử He là \(E_n=-\frac{2\pi^2m_ee^4}{h^2}\frac{Z^2}{n^2}=-\frac{8\pi^2m_ee^4}{h^2}\frac{1}{n^2}\) theo đơn vị erg với \(1erg=0.624146.10^{12}eV\)
quy đổi ra eV ta có \(E_n=-13.6\frac{4}{n^2}eV\)
Hàm sóng toàn phần \(\Psi\left(\vec{r_1,}\vec{r_2}\right)=\psi_{n_1,l_1,m_1}\left(\vec{r_1}\right)\psi_{n_2,l_2,m_2}\left(\vec{r_2}\right)\) trong đó các hàm sóng thành phần thu được nhờ việc giải từng phương trình. Ở đây việc giải phương trình cho từng hệ 1e trong tọa độ cầu đã thu được kết quả \(\psi_{n,l,m}\left(r,\Theta,\varphi\right)=R_{n,l}\left(r\right)\Theta_{l,m}\left(\theta\right)\Phi_m\left(\varphi\right)\), trong đó \(R_{n,l}\left(r\right)\) là hàm chỉ phụ thuộc r, gọi là hàm bán kính, chứa các tham số n, \(l\) mà ta gọi là số lượng tử chính n và số lượng tử orbita \(l\).
các hàm \(\Theta,\Phi\) phụ thuộc các góc \(\theta,\varphi\) nên gọi là hàm góc, chứa các tham số \(l,m\) ở đây m được gọi là số lượng tử từ.
a)\(\widehat{H}\)=\(\widehat{T}\)+U
\(^{ }_{ }\widehat{T}\)=\(\frac{-h^2}{8m\pi^2}\)(\(\Delta_1^2\)+\(\Delta_2^2\))
\(\Delta_1^2\)=\(\frac{\partial^2}{\partial x_1^2}\)+\(\frac{\partial^2}{\partial y_1^2}\)+\(\frac{\partial^2}{\partial z^2_1}\)
\(\Delta_2^{2_{ }}\)=\(\frac{\partial^2}{\partial x_2^2}\)+\(\frac{\partial^2}{\partial y_2^2}\)+\(\frac{\partial^2}{\partial z^2_2}\)
U=-\(\frac{2e^2}{r_{1a}}\)-\(\frac{2e^2}{r_{2a}}\)+\(\frac{2e^2}{r_{12}}\)
trong đó: r1a là khoảng cách từ e1 đến hạt nhân He
r2a là khoảng cách từ e2 đến hạt nhân He
r12 là khoảng cách giữa 2 e
\(\Rightarrow\)Pt schrodinger của nguyên tử He ở trạng thái dừng:
+\(\frac{\partial^2}{\partial z^2_2}\))- 2e2(\(\frac{1}{r_{1a}}\)+\(\frac{1}{r_{2a}}\)-\(\frac{1}{r_{12}}\))] \(\Psi\)=E\(\Psi\)
b)Giải pt khi giả thiết bỏ qua lực đẩy 2 e:
U=-\(\frac{2e^2}{r_{1a}}\)-\(\frac{2e^2}{r_{2a}}\)
E=\(\frac{-2\pi^2z^2m_ee^4}{h^2n^2}\)=\(\frac{-2\pi^2\cdot2^2m_ee^4}{h^2}\)=\(\frac{-8\pi^2m_ee^4}{h^2}\)(eV)