chứng minh các đẳng thức sau :
a) 128 . 912 = 1816
b) 7520 = 4510 . 530
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 8:
a) \(2^{225}=\left(2^3\right)^{75}=8^{75}\)
\(3^{150}=\left(3^2\right)^{75}=9^{75}\)
Vì \(8^{75}< 9^{75}\Rightarrow2^{225}< 3^{150}\)
b) \(2^{91}=\left(2^{13}\right)^7=8192^7\)
\(5^{35}=\left(5^5\right)^7=3125^7\)
Vì \(8192^7>3125^7\Rightarrow2^{91}>5^{35}\)
c) \(99^{20}=\left(99^2\right)^{10}=9801^{10}< 9999^{10}\)

7520 = 4510.530
Ta có: 4510.530 = (9.5)10.530 = 910.510.530 = (32)10.540
=320.(52)20 = 320.2520 = (3.25)20 = 7520
Vế phải bằng vế trái nên đẳng thức được chứng minh

a)128.912=(22.3)8.(32)12=216.38.324=216.332=216.(32)16=216.916=(2.9)16=1816
=>128.912=1816
b)7520=(3.52)20=320.540=(32)10.510.530=910.510.530=(9.5)10.530=4510.530
=>7520=4510.530


a) \(sin^4x+cos^4x=\left(sin^2x\right)^2+\left(cos^2x\right)^2\)
\(=\left(sin^2x\right)^2+2sin^2xcos^2x+\left(cos^2x\right)^2-2sin^2xcos^2x\)
\(=\left(sin^2x+cos^2x\right)^2-2sin^2xcos^2x\)
\(=1-2sin^2xcos^2x\)
b) \(\dfrac{1+cotx}{1-cotx}=\dfrac{tanx.cotx+cotx}{tanx.cotx-cotx}\)
\(=\dfrac{cotx.\left(tanx+1\right)}{cotx.\left(tanx-1\right)}\)
\(=\dfrac{tanx+1}{tanx-1}\)
c) \(\dfrac{cosx+sinx}{cos^3x}=\dfrac{1}{cos^2x}+\dfrac{tanx}{cos^2x}\)
\(=1+tan^2x+tanx.\dfrac{1}{cos^2x}\)
\(=1+tan^2x+tanx.\left(1+tan^2x\right)\)
\(=1+tan^2x+tanx+tan^3x\)
\(=tan^3x+tan^2x+tanx+1\)

Lời giải:
a.
$\sin ^4x+\cos ^4x=(\sin ^2x+\cos ^2x)^2-2\sin ^2x\cos ^2x$
$=1-2\sin ^2x\cos ^2x$
b.
$\frac{1+\cot x}{1-\cot x}=\frac{1+\frac{\cos x}{\sin x}}{1-\frac{\cos x}{\sin x}}=\frac{\cos x+\sin x}{\sin x-\cos x}(1)$
$\frac{\tan x+1}{\tan x-1}=\frac{\frac{\sin x}{\cos x}+1}{\frac{\sin x}{\cos x}-1}=\frac{\cos x+\sin x}{\sin x-\cos x}(2)$
Từ $(1); (2)$ ta có đpcm
c.
$\frac{\cos x+\sin x}{\cos ^3x}=(1+\frac{\sin x}{\cos x}).\frac{1}{\cos ^2x}$
$=(1+\tan x).\frac{\sin ^2x+\cos ^2x}{\cos ^2x}$
$=(1+\tan x)(\tan ^2x+1)=\tan ^3x+\tan ^2x+\tan x+1$
Ta có đpcm.

b) \(\left(\dfrac{\sqrt{14}-\sqrt{7}}{1-\sqrt{2}}+\dfrac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}\right):\dfrac{1}{\sqrt{7}-\sqrt{5}}\)
\(=\left(\dfrac{\sqrt{7}\left(\sqrt{2}-1\right)}{1-\sqrt{2}}+\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{1-\sqrt{3}}\right).\left(\sqrt{7}-\sqrt{5}\right)\)
\(=\left(-\sqrt{7}-\sqrt{5}\right).\left(\sqrt{7}-\sqrt{5}\right)=-\left(\sqrt{7}+\sqrt{5}\right)\left(\sqrt{7}-\sqrt{5}\right)\)
\(=-\left(7-5\right)=-2\)
c) \(\dfrac{a\sqrt{b}+b\sqrt{a}}{\sqrt{ab}}:\dfrac{1}{\sqrt{a}-\sqrt{b}}=\dfrac{\sqrt{ab}\left(\sqrt{a}+\sqrt{b}\right)}{\sqrt{ab}}.\left(\sqrt{a}-\sqrt{b}\right)\)
\(=\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)=a-b\)
d) \(\left(1+\dfrac{a+\sqrt{a}}{\sqrt{a}+1}\right)\left(1-\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)\)
\(=\left(1+\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)}{\sqrt{a}+1}\right)\left(1-\dfrac{\sqrt{a}\left(\sqrt{a}-1\right)}{\sqrt{a}-1}\right)\)
\(=\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right)=1-a\)
b) \(\left(\dfrac{\sqrt{14}-\sqrt{7}}{1-\sqrt{2}}\dfrac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}\right):\dfrac{1}{\sqrt{7}-\sqrt{5}}\)
\(=\left(\dfrac{\sqrt{7}\left(\sqrt{2}-1\right)}{1-\sqrt{2}}+\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{1-\sqrt{3}}\right).\left(\sqrt{7}-\sqrt{5}\right)\)
\(=\left(-\sqrt{7}+\left(-\sqrt{5}\right)\right).\left(\sqrt{7}-\sqrt{5}\right)=-\left(\sqrt{7}+\sqrt{5}\right)\left(\sqrt{7}-\sqrt{5}\right)=-2\)

Biến đổi vế trái:
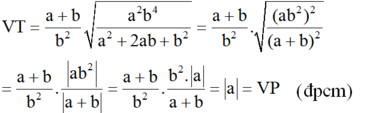
(vì a + b > 0 nên |a + b| = a + b; b2 > 0)
a) 128 . 912
= (3.4)8 . (32)12
= 38.48.324
= 332.48
= 332.(22)8
= 332.216 (*)
1816 = (32.2)16 = 332.216 (**)
(*)(**) => đpcm
phần b phân tích tương tự