Một vật nhỏ dao động điều hòa có biên độ 10 cm, tần số 0,5 Hz, ở thời điểm ban đầu t = 0 vật qua vị trí có li độ -5cm
theo chiều dương. Thời điểm đầu tiên vật qua vị trí có li độ cm theo chiều dương kể từ t = 0 là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
10 tháng 1 2018
- Biên độ dao động của vật:
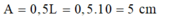
- Tần số góc của dao động:
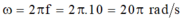
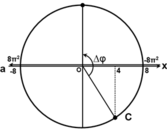
- Gốc thời gian được chọn là lúc vật đi qua vị trí: x = -A/2 = -2,5cm theo chiều dương của trục tọa độ:
2
24 tháng 9 2023
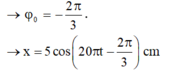
`a)A=4 (cm)`
`\omega=2\pi .f=10\pi (rad//s)`
Tại `t=0` thì `x_0 =-4=>\varphi=\pi (rad)`
`=>` Ptr: `x=4cos(10\pi t+\pi)`.
`b)` Ta có: `t=T/4 -T/6=T/12 =1/12 . [2\pi]/[10\pi]=1/60 (s)`
`c)T=[2\pi]/[10\pi]=0,2(s)`
`=>` Trong `2s` vật đi được `t=2/[0,2]=10T`
`=>` Quãng đường đi được trong `2s` là: `s=10.4.A=160(cm)`.
HQ
Hà Quang Minh
Giáo viên
29 tháng 7 2023
Có: \(f=\dfrac{w}{2\pi}=10\Rightarrow w=20\pi\)
Phương trình dao động của vật là:
\(x=4cos\left(20\pi t-\dfrac{\pi}{2}\right)\)
VT
14 tháng 11 2018
Thời điểm đầu tiên vật qua vị trí có li độ x = -12 cm
Tốc độ của vật tại thời điểm t = 2/3 s
⇒ v ≈ 0,33 m/s
1 tháng 11 2023
Câu 1.
a)Tốc độ góc: \(\omega=2\pi f=2\pi\)
Ta có: \(A=\sqrt{x^2+\dfrac{v^2}{\omega^2}}=\sqrt{0,05^2+\dfrac{\left(0,10\pi\right)^2}{\left(2\pi\right)^2}}=\dfrac{\sqrt{2}}{20}m\)
b)Phương trình vận tốc:
\(v=-\omega Asin\left(\omega t+\varphi\right)=-2\pi\cdot\dfrac{\sqrt{2}}{20}sin\left(2\pi t\right)\)
Câu 2.
a)Chu kỳ: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{5\pi}=0,4s\)
b)Li độ tại thời điểm \(t=2s:\)
\(x=2cos\left(5\pi t+\dfrac{\pi}{3}\right)=2cos\left(5\pi\cdot2+\dfrac{\pi}{3}\right)=1\)
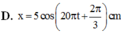
thiếu dữ kiện li độ sau rồi bạn ơi :))