Giải giúp bài 3 a
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 10 2021
\(a,=\dfrac{2}{3}\cdot\dfrac{21}{4}+\dfrac{5}{8}=\dfrac{7}{2}+\dfrac{5}{8}=\dfrac{33}{8}\\ b,=\left(\dfrac{1}{27}\cdot27\right)^{2020}\cdot27=1^{2020}\cdot27=27\\ c,=\dfrac{2^{30}\cdot2^{19}}{2^{48}}=2\)
KS
1
29 tháng 6 2019
a) \(\left(x+2y\right)^2=x^2+2.x.2y+\left(2y\right)^2=x^2+4xy+4y^2\)
b) \(\left(3-x\right).\left(3+x\right)=9+3x-3x-x^2=9-x^2=3^2-x^2\)
c) \(\left(5-x\right)^2=5^2-2.5.x+x^2=25-10x+x^2\)
d) \(\left(3+y\right)^2=3^2+2.3.y+y^2=9+6y+y^2\)
30 tháng 3 2021
Ta có: \(\dfrac{a}{b}=\dfrac{3}{5}\)
\(\Leftrightarrow\dfrac{a}{3}=\dfrac{b}{5}\)
Đặt \(\dfrac{a}{3}=\dfrac{b}{5}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=3k\\b=5k\end{matrix}\right.\)
Ta có: \(\dfrac{2a-4b}{a-5b}\)
\(=\dfrac{2\cdot3k-4\cdot5k}{3k-5\cdot5k}=\dfrac{6k-20k}{3k-25k}\)
\(=\dfrac{-14k}{-22k}=\dfrac{7}{11}\)
VP
0
21 tháng 6 2017
B1: để x là số nguyên thì: 5 chia hết cho 2x+1
=> \(2x+1\in U\left(5\right)\)
+> \(2x+1\in\left\{1;-1;5;-5\right\}\)
=> \(x\in\left\{0;-1;2;-3\right\}\)
2H
1
OY
28 tháng 9 2021
a) Vì \(\left|2x+4\right|\ge0;\left|y\right|\ge0\)
mà \(\left|2x+4\right|+\left|y\right|=0\)
\(\Rightarrow\left\{{}\begin{matrix}\left|2x+4\right|=0\\\left|y\right|=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=-2\\y=0\end{matrix}\right.\)
Vậy \(\left(x;y\right)=\left(-2;0\right)\)
26 tháng 1 2017
Bài 2:Ta có:\(a+7⋮a\)
\(\Rightarrow7⋮a\)
\(\Rightarrow a\inƯ\left(7\right)\)
\(Ư\left(7\right)=1;-1;7;-7\)
Suy ra \(a\in1;-1;7;-7\)
bà 3:\(a+1⋮a-2\)
\(a-2+3⋮a-2\)
\(3⋮a-2\)
\(\Rightarrow a-2\inƯ\left(3\right)\)
\(Ư\left(3\right)=1;3\);-1;-3
Suy ra:\(a\in3;5;1;-1.\)
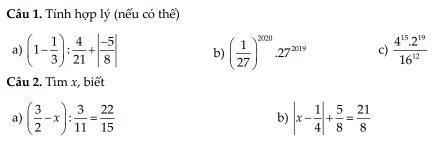
a, \(A=\frac{1}{\sqrt{4+\sqrt{10+2\sqrt{5}}}+\sqrt{4-\sqrt{10+2\sqrt{5}}}}\)
\(=\frac{\sqrt{4+\sqrt{10+2\sqrt{5}}}-\sqrt{4-\sqrt{10+2\sqrt{5}}}}{4+\sqrt{10+2\sqrt{5}}-4+\sqrt{10+2\sqrt{5}}}\)
\(=\frac{\sqrt{4+\sqrt{10+2\sqrt{5}}}-\sqrt{4-\sqrt{10+2\sqrt{5}}}}{2\sqrt{10+2\sqrt{5}}}\)
\(A^2=\frac{4+\sqrt{10+2\sqrt{5}}-2\sqrt{16-10-2\sqrt{5}}+4-\sqrt{10+2\sqrt{5}}}{4\left(10+2\sqrt{5}\right)}\)
\(=\frac{8-2\sqrt{6-2\sqrt{5}}}{40+8\sqrt{5}}=\frac{9-2\left(\sqrt{5}-1\right)}{40+2.4\sqrt{5}}\)
\(\Rightarrow A=\sqrt{\frac{11-2\sqrt{5}}{40+8\sqrt{5}}}=\frac{\sqrt{11-2\sqrt{5}}}{2\sqrt{10+2\sqrt{5}}}=\frac{\sqrt{\left(11-2\sqrt{5}\right)\left(10+2\sqrt{5}\right)}}{20+4\sqrt{5}}\)
\(=\frac{\sqrt{110+2\sqrt{5}-20}}{20+4\sqrt{5}}=\frac{\sqrt{90+2\sqrt{5}}}{20+4\sqrt{5}}\)
trục căn thức cho biểu thức mất căn là được
Sửa
\(A^2=\frac{1}{4+\sqrt{10+2\sqrt{5}}+2\sqrt{16-10-2\sqrt{5}}+4-\sqrt{10+2\sqrt{5}}}\)
\(=\frac{1}{8+2\sqrt{6-2\sqrt{5}}}=\frac{1}{8+2\left(\sqrt{5}-1\right)}=\frac{1}{6+2\sqrt{5}}\)
\(\Rightarrow A=\frac{1}{\sqrt{5}+1}=\frac{\sqrt{5}-1}{4}\)