CMR: các tia phân giác cảu các góc của 1 hình chữ nhật cắt nhau tạo thành 1 hình chữ nhật (2 cạnh kề của hình chữ nhật ko = nhau)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
3 tháng 8 2018
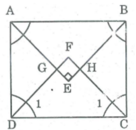
Gọi giao điểm các đường phân giác của các góc: A, B, C, D theo thứ tự cắt nhau tại E, H, F, G.
* Trong ∆ ADG , ta có:
∠ (GAD) = 45 0 ; ∠ (GDA) = 45 0 (gt)
Suy ra: ∠ (AGD) = 180 0 - ∠ (GAD) - ∠ (GDA) = 90 0
⇒ ∆ GAD vuông cân tại G.
⇒ GD = GA
Trong ∆ BHC, ta có:
∠ (HBC) = 45 0 ; ∠ (HCB) = 45 0 (gt)
Suy ra: ∠ (BHC) = 180 0 - ∠ (HBC) - ∠ (HCB) = 90 0
⇒ ∆ HBC vuông cân tại H.
⇒ HB = HC
* Trong ΔFDC, ta có: ∠ D 1 = 45 0 ; ∠ C 1 = 45 0 (gt)
Suy ra: ∠ F = 180 0 - D1 - C1 = 90 0
⇒ ∆ FDC vuông cân tại F ⇒ FD = FC
Nên tứ giác EFGH là hình chữ nhật (vì có 3 góc vuông).
Xét ∆ GAD và ∆ HBC,ta có: ∠ (GAD) = ∠ (HBC) = 45 0
AD = BC (tính chất hình chữ nhật)
∠ (GDA) = ∠ (HCB) = 45 0
Suy ra: ∆ GAD = ∆ HBC ( g.c.g)
Do đó, GD = HC .
Lại có: FD = FC (chứng minh trên)
Suy ra: FG = FH
Vậy hình chữ nhật EFGH có hai cạnh kề bằng nhau nên nó là hình vuông.
PT
1
CM
27 tháng 9 2017
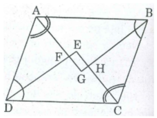
Gọi G, H, E, F lần lượt là giao điểm của các đường phân giác của ∠ A và ∠ B; ∠ B và ∠ C; ∠ C và ∠ D; ∠ D và ∠ A
Ta có: ∠ (ADF) = 1/2 ∠ (ADC) (gt)
∠ (DAF) = 1/2 ∠ (DAB) (gt)
∠ (ADC) + ∠ (DAB) = 180 0 (hai góc trong cùng phía)
Suy ra: ∠ (ADF) + ∠ (DAF) = 1/2 ( ∠ (ADC) + ∠ (DAB) ) = 1/2 . 180 0 = 90 0
Trong ∆ AFD, ta có:
∠ (AFD) = 180 0 – ( ∠ (ADF) + ∠ (DAF)) = 180 0 – 90 0 = 90 0
∠ (EFG) = ∠ (AFD) (đối đỉnh)
⇒ ∠ (EFG) = 90 0
∠ (GAB) = 1/2 ∠ (DAB) (gt)
∠ (GBA) = 1/2 ∠ (CBA) (gt)
∠ (DAB) + ∠ (CBA) = 180 0 (hai góc trong cùng phía)
⇒ ∠ (GAB) + ∠ (GBA) = 1/2 ( ∠ (DAB) + ∠ (CBA) ) = 1/2 . 180 0 = 90 0
Trong ΔAGB ta có: ∠ (AGB) = 180 0 – ( ∠ (GAB) + ∠ (GBA) ) = 180 0 - 90 0 = 90 0
Hay ∠ G = 90 0
∠ (EDC) = 1/2 ∠ (ADC) (gt)
∠ (ECD) = 1/2 ∠ (BCD) (gt)
∠ (ADC) + ∠ (BCD) = 180 0 (hai góc trong cùng phía)
⇒ ∠ (EDC) + ∠ (ECD) = 1/2 (∠ ∠ ADC) + ∠ (BCD) ) = 1/2 . 180 0 = 90 0
Trong ΔEDC ta có: ∠ (DEC) = 180 0 – ( ∠ (EDC) + ∠ (ECD) ) = 180 0 - 90 0 = 90 0
Hay ∠ E = 90 0
Vậy tứ giác EFGH là hình chữ nhật (vì có ba góc vuông).