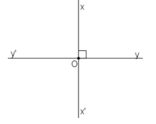
Hai đường thẳng xx' và yy' cắt nhau ở D . Tính góc xDy và góc yDx'
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 6 2019
Ta có :
\(\widehat{xOy}+2.\widehat{x'Oy}=180^o\) ( hai góc kề bù )
\(\widehat{xOy}+\widehat{xOy}=180^o\)
\(\widehat{xOy}.2=180^o\)
\(\Rightarrow\widehat{xOy}=\frac{180^o}{2}=90^o\)
Do \(\widehat{xOy}\)và \(\widehat{x'Oy'}\) là hai góc đối đỉnh mà \(\widehat{xOy}=90^o\Rightarrow\widehat{x'Oy'}=90^o\)
Vậy \(\widehat{x'Oy'}=90^o\)
24 tháng 6 2019
Ta có xOy + x'Oy = 180 độ
Mà xOy = 2 x'Oy
=> 2 x'Oy + x'Oy = 180 độ => 3 x'Oy = 180 độ
=> x'Oy = 180 : 3 = 60 độ => xOy = 180 - 60 = 120 độ
Mà xOy = x'Oy' =120 độ ( đối đỉnh)
CM
27 tháng 8 2017
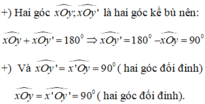
Do đó, mỗi đường thẳng là đường phân giác của một góc bẹt.
a. Đúng
b. Đúng
c. Đúng
3 tháng 10 2021
a, Nếu tia At không cắt yy'
=> At // yy'
=> At trung với Ax (vì xx' // yy')
Mà At là phân giác góc xAb
=> At nằm giữa Ax và AB
=> At không trùng Ax
=> At cắt yy'
b,
Bạn xem lại đề. C ở đâu vậy?
TA
6 tháng 8 2021
Ta có: `\hat(xAy)=\hat(x'Ay')=40^@` (đối đỉnh)
`\hat(y'Ax)+\hat(xAy)=180^@ => \hat(y'Ax)=180^@-\hat(xAy)=180^@-40^@=140^@`
NH
23 tháng 7 2017
a) Hai đường thẳng xx' và yy' cắt nhau tại O : Đúng
b) Hai đường thẳng xx' và yy' tạo thành 4 góc vuông : Sai
c) Mỗi đường thẳng là đường phân giác của một góc bẹt : Đúng
