Cho x là số thực. Tìm giá trị nhỏ nhất của \(P=x^4+3y^4-xy^3-x^3y+2021\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt \(\left\{{}\begin{matrix}\sqrt{2x+3}=a\ge0\\\sqrt{y}=b\ge0\end{matrix}\right.\)
\(\Rightarrow b\left(b^2+1\right)-3a^2=\left(a^2+1\right)a-3b^2\)
\(\Rightarrow a^3-b^3+3a^2-3b^2+a-b=0\)
\(\Leftrightarrow\left(a-b\right)\left(a^2+ab+b^2\right)+\left(a-b\right)\left(3a+3b\right)+a-b=0\)
\(\Leftrightarrow\left(a-b\right)\left(a^2+ab+b^2+3a+3b+1\right)=0\)
\(\Leftrightarrow a=b\Rightarrow\sqrt{2x+3}=\sqrt{y}\)
\(\Rightarrow y=2x+3\)
\(\Rightarrow M=x\left(2x+3\right)+3\left(2x+3\right)-4x^2-3\) tới đây chắc chỉ cần bấm máy

Đặt \(x+y=t,t\in\left[-2;2\right]\)
Biến đổi được \(P=-2t^3+6t\)
Xét \(f\left(t\right)=-2t^3+6t\) trên \(\left[-2;2\right]\)
Lập bảng biến thiên
Ta có \(P_{Max}=4\) khi t=1
\(P_{Min}=-4\) khi t= -1
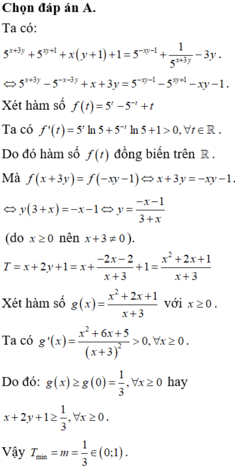
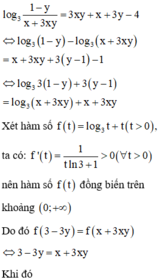
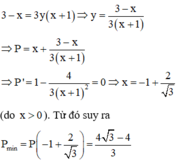
\(P=x^4+3y^4-xy^3-x^3y+2021\)
\(=x^3\left(x-y\right)-y^3\left(x-y\right)+4y^4+2021\)
\(=\left(x-y\right)\left(x^3-y^3\right)+4y^4+2021\)
\(=\left(x-y\right)^2\left(x^2+xy+y^2\right)+4y^2+2021\)
\(\Rightarrow P\ge2021\)\(\Rightarrow Pmin=2021\Leftrightarrow x=y=0\)