Chứng minh rằng với mọi số nguyên a ta có:
a.(a+1)+1>0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DP
2
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
a)
Trên nửa đường tròn đơn vị, lấy điểm M sao cho \(\widehat {xOM} = \alpha \)
Gọi H, K lần lượt là các hình chiếu vuông góc của M trên Ox, Oy.
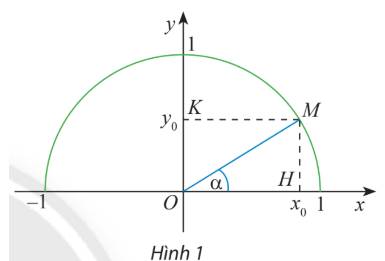
Ta có: tam giác vuông OHM vuông tại H và \(\alpha = \widehat {xOM}\)
Do đó: \(\sin \alpha = \frac{{MH}}{{OM}} = MH;\;\cos \alpha = \frac{{OH}}{{OM}} = OH.\)
\( \Rightarrow {\cos ^2}\alpha + {\sin ^2}\alpha = O{H^2} + M{H^2} = O{M^2} = 1\)
b) Ta có:
\(\begin{array}{l}\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}.\\ \Rightarrow \;\tan \alpha .\cot \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}.\frac{{\cos \alpha }}{{\sin \alpha }} = 1\end{array}\)
c) Với \(\alpha \ne {90^o}\) ta có:
\(\begin{array}{l}\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\\ \Rightarrow \;1 + {\tan ^2}\alpha = 1 + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{1}{{{{\cos }^2}\alpha }}\;\end{array}\)
d) Ta có:
\(\begin{array}{l}\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }};\;\\ \Rightarrow \;1 + {\cot ^2}\alpha = 1 + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{1}{{{{\sin }^2}\alpha }}\;\end{array}\)
2
27 tháng 4 2022
`a) 2 ( a^2 + b^2 ) >= ( a + b )^2`
`<=> 2a^2 + 2b^2 >= a^2 + 2ab + b^2`
`<=> a^2 - 2ab + b^2 >= 0`
`<=> ( a - b )^2 >= 0` (Luôn đúng `AA a,b`)
`=>` Đẳng thức được c/m
_________________________________________
`b) a^2 + b^2 + c^2 >= ab + bc + ca`
`<=> 2a^2 + 2b^2 + 2c^2 >= 2ab + 2bc + 2ca`
`<=> ( a^2 - 2ab + b^2 ) + ( b^2 - 2bc + c^2 ) + ( c^2 - 2ca + a^2 ) >= 0`
`<=> ( a - b )^2 + ( b - c )^2 + ( c - a )^2 >= 0` (Luôn đúng `AA a,b,c`)
`=>` Đẳng thức được c/m
TH1: a là số tự nhiên ⇒ a ≥ 0 ⇒ a + 1 > 0
⇒ a. (a + 1) > 0 ⇒ a. (a + 1) + 1 > 0
TH2: a là số nguyên âm và a ≤ -2 ⇒ a + 1 < 0
⇒ a. (a + 1) > 0 ⇒ a. (a + 1) + 1 > 0
TH3: a = -1 ⇒a. (a + 1) + 1 = -1.0 + 1 = 1 > 0
Ta có: \(a\left(a+1\right)+1\)
\(=a^2+a+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(a+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\forall a\)