Trên một khúc sông với hai bờ song song với nhau, một người lái đò dự
định chèo đò qua sông từ vị trí A ở bờ bên này sang vị trí B ở bờ bên kia, đường thẳng AB vuông góc với các bờ sông. Người lái đò đã xuất phát từ A và lái đò theo phương vuông góc với bờ sông, do đó con đò bị dòng nước đẩy xiên và cập bến ở bờ bên kia tại vị trí C cách B một đoạn 45 m. Biết khúc sông rộng 270 m, hỏi dòng nước đã đẩy chiếc đò lệch một góc có số đo bằng bao nhiêu so với phương AB? (làm tròn kết quả đến phút).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

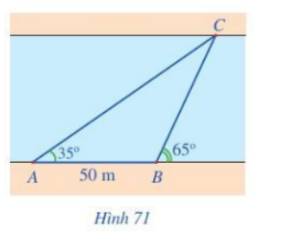
Ta có: \(\widehat C = {65^o} - {35^o} = {30^o}\)(tính chất góc ngoài)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}} \Rightarrow AC = \frac{{AB.\sin B}}{{\sin C}}\)
\( \Leftrightarrow AC = \frac{{50.\sin ({{180}^o} - {{65}^o})}}{{\sin {{30}^o}}} \approx 90,63.\)
Độ rộng của khúc sông là: \(AC.\sin A = 90,63.\sin {35^o} \approx 52\;(m)\)

Đáp án C.
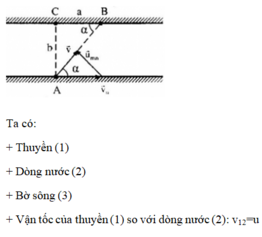
Lúc này theo hình vẽ ta có:
v t b = v t n 2 + v n b 2 = 10 m / s

Đáp án C.
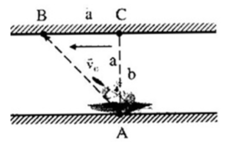
Lúc này theo hình vẽ ta có: v t b = v t n 2 + v n b 2 = 10 m / s

Đáp án B.
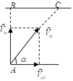
Trong khoảng thời gian thuyền đi ngang từ A đến B ,
nước đi dọc từ B đến C nên ta có A B B C = v t n v n b = 3 ⇒ B C = A B 3 = 20 m