Cách nào để chuyển từ: \(ad=bc\rightarrow\frac{a}{b}=\frac{c}{d}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 4 2020
Bài 1:
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{b}=\frac{c}{d}=\frac{a+c}{b+d}=\frac{a-c}{b-d}\)
\(\Rightarrow\frac{a}{b}=\frac{a+c}{b+d}=\frac{a-c}{b-d}\)(đpcm)
23 tháng 8 2018
Trước hết ta xét \(\frac{a}{b}=\frac{c}{d}\Rightarrow ad=bc\)
Vì ở đây a,b,c,d đều là những số dương nên khi nhân chéo thì bất đẳng thức không đổi dấu
Do đó \(\frac{a}{b}< \frac{c}{d}\Rightarrow ad< bc\)( nhân chéo tử của phân số này với mẫu phân số kia )
Trường hợp 1 số là số âm thì bất đẳng thức đổi dấu
23 tháng 8 2018
\(\frac{a}{b}< \frac{c}{d}< =>\frac{ad}{bd}< \frac{bc}{bd}=>ad< bc.\)
3 tháng 10 2015
Còn nha. Đặt \(\frac{a}{b}=\frac{c}{d}=k\Rightarrow a=bk;c=dk\)
Ta có: \(\frac{\left(a+b\right)^2}{\left(c+d\right)^2}=\frac{\left(bk+b\right)^2}{\left(dk+d\right)^2}=\frac{b^2.\left(k+1\right)^2}{d^2.\left(k+1\right)^2}=\frac{b^2}{d^2}^{\left(1\right)}\)
Lại có: \(\frac{a^2+b^2}{c^2+d^2}=\frac{b^2.k^2+b^2}{d^2.k^2+d^2}=\frac{b^2.\left(k^2+1\right)}{d^2.\left(k^2+1\right)}=\frac{b^2}{d^2}^{\left(2\right)}\)
Từ (1) và (2) => đpcm
3 tháng 2 2017
\(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}\)
Áp dụng TC DTSBN ta có :
\(\frac{a}{c}=\frac{b}{d}=\frac{a+b}{c+d}=\frac{a-b}{c-d}\Rightarrow\frac{a+b}{a-b}=\frac{c+d}{c-d}\) ( đpcm )
21 tháng 1 2018
Vẽ MK vuông góc với AB,MH vuông góc AC
Suy ra:MH=MK(t/c tia phân giác của một góc)
sABC=sABM+sACM
1/2b.c=1/2d.b +1/2d.c
1/2b.c=1/2(b+c)
b.c=d.(b+c)
Suy ra d=bc/b+c (đpcm)
Chúc bạn học tốt nhe!!! :3
HQ
Hà Quang Minh
Giáo viên
13 tháng 9 2023
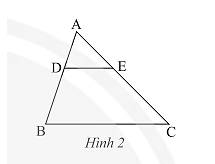
Vì \(DE//BC\) nên theo định lí Thales và hệ quả của định lí Thales ta có:
\(\frac{{AD}}{{BD}} = \frac{{AE}}{{EC}};\frac{{BD}}{{AD}} = \frac{{EC}}{{AE}};\frac{{BD}}{{AB}} = \frac{{EC}}{{AC}};\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}} = \frac{{DE}}{{BC}}\).
22 tháng 11 2016
Ta có: \(\frac{a}{b}\)=\(\frac{c}{d}\)
+ \(\frac{a}{b}\)=\(\frac{a}{b}\).\(\frac{a}{b}\)=\(\frac{a^2}{b^2}\) (1)
+ \(\frac{a}{b}\)=\(\frac{c}{d}\)=\(\frac{ac}{bd}\) (2)
Từ (1); (2) => \(\frac{a}{b}\)=\(\frac{c}{d}\)=>\(\frac{a^2}{b^2}\)=\(\frac{ac}{bd}\)
22 tháng 11 2016
Ta có \(\frac{a}{b}=\frac{c}{d}\Rightarrow\left(\frac{a}{b}\right)^2=\frac{a^2}{b^2}=\left(\frac{c}{d}\right)^2=\frac{a.c}{b.d}\left(ĐPCM\right)\)
C1: Phân số bằng nhau
C2: Tỉ lệ thức
Mik cũng ko rõ, trả lời đại nha
HOK TỐT\(\text{ad = bc}\)
\(\Rightarrow\frac{ad}{bd}=\frac{bc}{bd}\Rightarrow\frac{a}{b}=\frac{c}{d}\)