Trên 2 đỉnh của tam giác ABC ( AB = 4 cm, AC = 3 cm, BC =5 cm) người ta đặt 2 điện tích qB = 5.10^– 8 C và qC= -10.10^– 8 C. Hỏi vectơ cường độ điện trường tại A sẽ hợpvới cạnh AC một góc bằng bao nhiêu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tại B có 2 cường độ điện trường thành phần EA Ec (vecto)
EA = 16.105 (V/m) EC = 6,75.105 (V/m)
EB = EA + EC (vecto)
Độ lớn: EB2 = EA2 + EC2 => EB = 1734618,114 (V/m)

Chọn: A
Hướng dẫn:
- Cường độ điện trường do điện tích q 1 = 5 . 10 - 16 (C) nằm tại B gây ra tại A có độ lớn là:
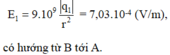
- Cường độ điện trường do điện tích q 2 = 5 . 10 - 16 (C) nằm tại C gây ra tại A có độ lớn
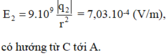
- Cường độ điện trường tổng hợp tại điểm A là


a) Cường độ điện trường do điện tích Q1 gây ra tại A là:
\(E_1=\dfrac{\left|Q_1\right|}{4\pi\varepsilon_0AB^2}=\dfrac{5\cdot10^{-5}}{4\pi\varepsilon_0}\)(V/m)
Cường độ điện trường do điện tích Q2 gây ra tại A là:
\(E_2=\dfrac{\left|Q_2\right|}{4\pi\varepsilon_0AC^2}=\dfrac{25\cdot10^{-6}}{4\pi\varepsilon_0}\)(V/m)
b) Mà ta có:
\(E_1\perp E_2\Rightarrow E=\sqrt{E^2_1+E^2_2}=463427\left(V/m\right)\)
Cường độ điện trường của điện tích ở C đối với điểm A là hướng vô
Cường độ điện trường của điện tích ở B đối với điểm A là hướng ra
\(\Rightarrow\overrightarrow{E_{BA}}\perp\overrightarrow{E_{CA}}\)
\(E_{BA}=\dfrac{k\left|q_B\right|}{AB^2};E_{CA}=\dfrac{k\left|q_C\right|}{AC^2}\)
\(\Rightarrow\tan\left(\widehat{\overrightarrow{E_A};\overrightarrow{AC}}\right)=\dfrac{E_{BA}}{E_{CA}}=...\Rightarrow\left(\widehat{\overrightarrow{E_A};\overrightarrow{AC}}\right)=...\)