Cho hình vuông ABCD có tâm O và cạnh bằng 6 cm. Điểm M thuộc BM.Khi BM=2cm,hạ OK vuông góc với AM tại K.Tính OK
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Xét (O) có
OK là một phần đường kính(OK là bán kính của (O))
AB là dây(gt)
OK⊥AB tại H
Do đó: H là trung điểm của AB(Định lí đường kính vuông góc với dây)
Xét tứ giác OAKB có
H là trung điểm của đường chéo AB(cmt)
H là trung điểm của đường chéo OK(gt)
Do đó: OAKB là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Hình bình hành OAKB có OA=OB(=R)
nên OAKB là hình thoi(Dấu hiệu nhận biết hình thoi)

Ta có: ΔBAO vuông tại A
=>ΔBAO nội tiếp đường tròn đường kính BO
=>A nằm trên đường tròn đường kính BO(1)
Ta có: ΔBMO vuông tại M
=>ΔBMO nội tiếp đường tròn đường kính BO
=>M nằm trên đường tròn đường kính BO(2)
Từ (1),(2) suy ra A,B,M,O cùng thuộc đường tròn đường kính BO

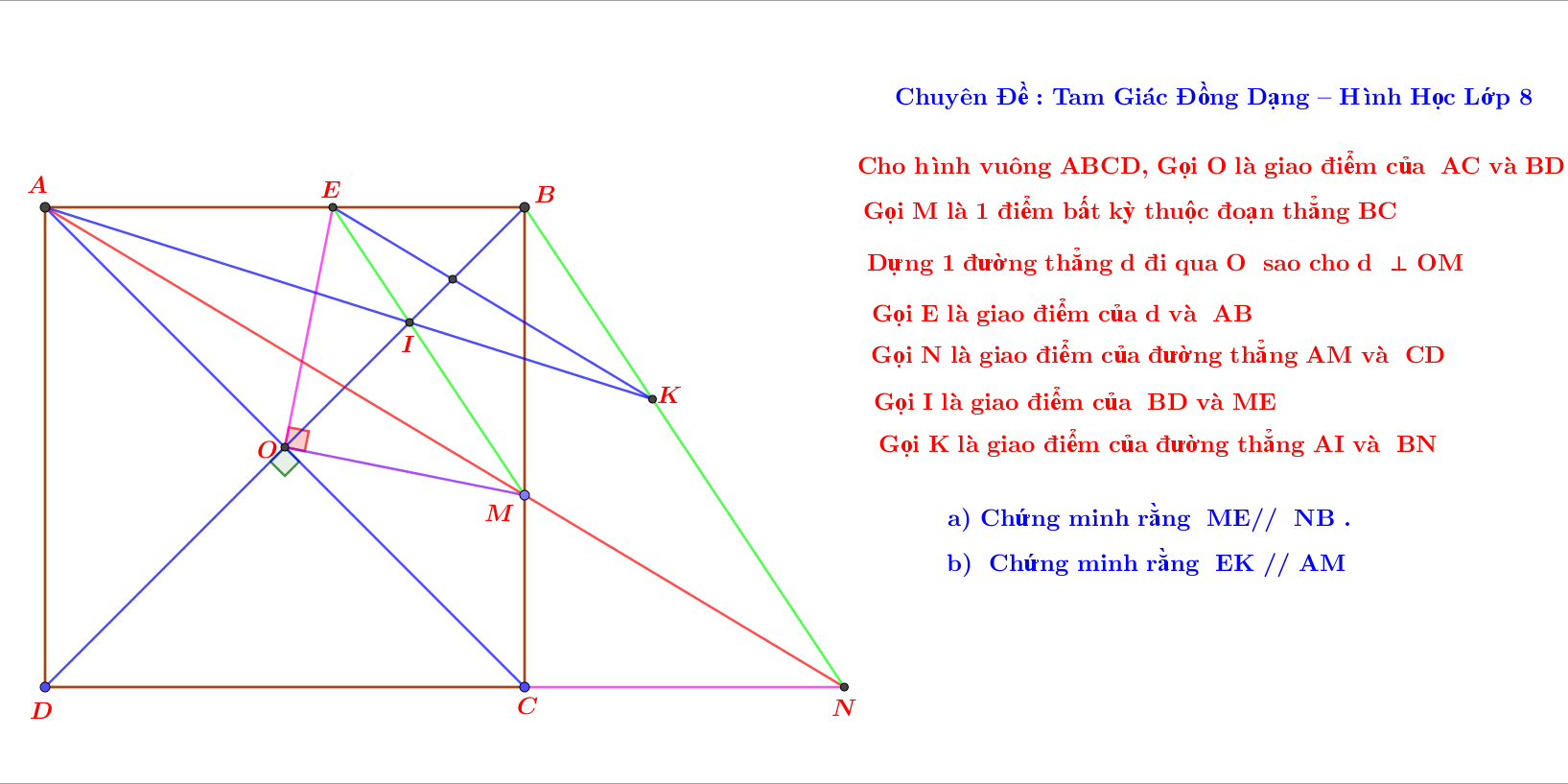
a. \(\widehat{AOE}=90^0-\widehat{BOE}=\widehat{BOM}\)
\(\Rightarrow\)△AOE=△BOM (g-c-g). \(\Rightarrow AE=BM;BE=CM\).
△MCN có: CN//AB \(\Rightarrow\dfrac{MN}{AM}=\dfrac{CM}{BM}=\dfrac{BE}{AE}\Rightarrow\)ME//NB.