Cho tam giác ABC vuông tại A, đường cao AH, đường trung tuyến AM.
a) Chứng minh rằng ∠(HAB) = ∠(MAC)
b) Gọi D, E theo thứ tự là chân đường vuông góc kể từ H đến AB, AC. Chứng
minh rằng AM vuông góc với DE.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 10 2019
a,Ta có :
\(AH\perp BC\left(GT\right)\Rightarrow\widehat{HAB}+\widehat{B}=90^o\)
Mà \(\widehat{B}+\widehat{C=90^o}\)( Trong tam giác vuông 2 góc nhọn phụ nhau )
\(\Rightarrow\widehat{HAB}=\widehat{C}\left(1\right)\)
Xét \(\Delta ABC\left(\widehat{BAC}=90^o\right)\)có :
AM là trung tuyến ứng với cạnh huyền BC ( GT )
\(\Rightarrow AM=MC=\frac{1}{2}BC\)( Tính chất )
Vì \(AM=MC\)
\(\Rightarrow\Delta AMC\)cân tại M ( Định nghĩa )
\(\Rightarrow\widehat{MAC}=\widehat{C}\)( Tính chất ) \(\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\Rightarrow\widehat{HAB}=\widehat{MAC}\left(DPCM\right)\)
CM
8 tháng 1 2017
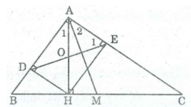
Xét tứ giác ADHE, ta có:
∠ A = 90 0 (gt)
∠ (ADH) = 90 0 (vì HD ⊥ AB)
∠ (AEH) = 90 0 (vì HE ⊥ AC)
Suy ra tứ giác ADHE là hình chữ nhật (vì có 3 góc vuông).
+ Xét ∆ ADH và ∆ EHD có :
DH chung
AD = EH ( vì ADHE là hình chữ nhật)
∠ (ADN) = ∠ (EHD) = 90 0
Suy ra: ∆ ADH = ∆ EHD (c.g.c)
⇒ ∠ A 1 = ∠ (HED)
Lại có: ∠ (HED) + ∠ E 1 = ∠ (HEA) = 90 0
Suy ra: ∠ E 1 + ∠ A 1 = 90 0
∠ A 1 = ∠ A 2 (chứng minh trên) ⇒ ∠ E 1 + ∠ A 2 = 90 0
Gọi I là giao điểm của AM và DE.
Trong ∆ AIE ta có: ∠ (AIE) = 180o – ( ∠ E 1 + ∠ A 2 ) = 180 0 - 90 0 = 90 0
Vậy AM ⊥ DE.
10 tháng 11 2021
a, Vì \(\widehat{AEH}=\widehat{ADH}=\widehat{DAE}=90^0\) nên AEHD là hcn
Do đó AH=DE
b, Vì \(\widehat{HAB}=\widehat{MCA}\) (cùng phụ \(\widehat{CAH}\))
Mà \(\widehat{MCA}=\widehat{MAC}\) (do \(AM=CM=\dfrac{1}{2}BC\) theo tc trung tuyến ứng ch)
Vậy \(\widehat{HAB}=\widehat{MAC}\)
c, Gọi O là giao AM và DE
Vì AEHD là hcn nên \(\widehat{HAB}=\widehat{ADE}\Rightarrow\widehat{MAC}=\widehat{ADE}\)
Mà \(\widehat{ADE}+\widehat{AED}=90^0\left(\Delta AED\perp A\right)\) nên \(\widehat{MAC}+\widehat{ADE}=90^0\)
Xét tam giác AOE có \(\widehat{AOE}=180^0-\left(\widehat{MAC}+\widehat{ADE}\right)=90^0\)
Vậy AM⊥DE tại O
CM
6 tháng 8 2019
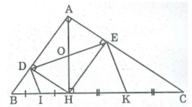
Xét tứ giác ADHE, ta có:
∠ A = 90 0 (gt)
∠ (ADH) = 90 0 (vì HD ⊥ AB)
∠ (AEH) = 90 0 (Vì HE ⊥ AC)
Suy ra tứ giác ADHE là hình chữ nhật (vì có 3 góc vuông)
Vậy AH = DE (tính chất hình chữ nhật)
11 tháng 8 2019
a) Xét ∆ vuông ABC có
AM là trung tuyến
=> AM = BM = CM
=> ∆AMC cân tại M
=> MAC = MCA
Xét ∆ABH có :
BHA + BAH + ABH = 180°
=> BAH + ABH = 90°
Xét ∆ABC có :
ABC + BCA + BAC = 180°
=> ABC + ACB = 90°
=> BAH = MCA
Mà MAC = MCA (cmt)
=> BAH = MAC
b) Gọi I là giao điểm DE và AH
Xét tứ giác DHEA có :
BAC = 90° (gt)
MDA = 90° ( MD\(\perp\)AB )
HEA = 90° ( HE\(\perp\)AC)
=> DHEA là hình chữ nhật
=> I là trung điểm DE và HA
=> DI = IA
=> ∆IDA cân tại I
=> IDA = IAD (1)
Vì MAC = MCA (2) (cmt)
Ta có :
DAI + MAC = 90°
MCA + MAC = 90°
=> DAI = MCA ( cùng phụ với MAC )(3)
Từ (1) (2)(3)
=> DAI = MAC = MCA
Vì I là trung điểm DE
=> ∆IAE cân tại I
=> IAE = IEA
Gọi giao điểm DE,AM là O
Xét ∆ADE có :
DAE + ADE + DEA = 180°
=> ADE + DEA = 90° .
Mà IAE = IEA (cmt)
MAC = ADI (cmt)
=> MAE + IEA = 90°
Xét ∆IAE có :
IAE + IEA + AIE = 180°
=> AIE = 90°
Hay AM \(\perp\)DE(dpcm)
16 tháng 12 2017
1a) A=D=E=90 độ
=>AEHD là hcn
=>AH=DE
b)Xét tam giác DBH vuông tại D có:
DI là đường trung tuyến ứng với cạnh huyền BH
=>DI=BH/2=IH
=>tam giác IDH cân tại I
=>góc IDH=góc IHD (1)
Gọi O là gđ 2 đường chéo AH và DE
=>OD=OA=OE=OH (tự c/m)
=> tam giác DOH cân tại O
=> góc ODH=góc OHD(2)
từ (1) và (2) => góc ODH+góc IDH=90 độ(EHD+DHI=90 độ)
=>IDvuông góc DE(3)
Cmtt ta được: KEvuông góc DE(4)
Từ (3)và (4) => DI//KE.
16 tháng 12 2017
2a) Ta có góc HAB+góc HAC=90 độ (1)
Xét tam giác ABC vuông tại A có
AM là đg trung tuyến ứng vs cạnh huyền BC
=>AM=MC
=>tam giác AMC cân
=>góc MAC=góc ACM
Lại có: góc HAC+góc ACH=90 độ(2)
Từ (1) và (2) => góc BAH=góc ACM
Mà góc AMC=góc MAC(cmt)
=>ABH=MAC(3)
b)A=D=E=90 độ
=>AFHE là hcn
Gọi O là gđ EF và AM
OA=OF(tự cm đi nha)
=>tam giác OAF cân
=>OAF=OFA(4)
Ta có : OAF+MCA=90 độ(5)
Từ (3)(4) và (5)
=>MAC+OFA=90 độ
Hay AM vuông góc EF
k giùm mình nha.
CM
26 tháng 12 2017
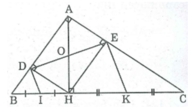
Tam giác BDH vuông tại D có DI là đường trung tuyến thuộc cạnh huyền BH
⇒ DI = IB = 1/2 BH (tính chất tam giác vuông)
⇒ ∆ IDB cân tại I ⇒ ∠ (DIB) = 180 0 - 2. ∠ B (1)
Tam giác HEC vuông tại E có EK là đường trung tuyến thuộc cạnh huyền HC.
⇒ EK = KH = 1/2 HC (tính chất tam giác vuông) .
⇒ ∆ KHE cân tại K ⇒ ∠ (EKH) = 180 0 - 2. ∠ (KHE) (2)
Tứ giác ADHE là hình chữ nhật nên:
HE // AD hay HE // AB ⇒ ∠ B = ∠ (KHE) (đồng vị)
Từ (1), (2) và (3) suy ra: ∠ (DIB) = ∠ (EKH)
Vậy DI // EK (vì có cặp góc đồng vị bằng nhau).