Tìm giá trị nhỏ nhất của:
F= x4-2x2+3
G=( x2+2)2-3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 5 2021
\(P=\left[\left(\dfrac{-1}{3}\right)^2x^3+\left(2x^2\right)^2+\dfrac{1}{2}\right]-\left[x\left(\dfrac{1}{3}x\right)^2+\dfrac{3}{2^3}+x^4\right]+\left(y-2013\right)^2=\left(\dfrac{1}{9}x^3+4x^4+\dfrac{1}{2}\right)-\left(\dfrac{1}{9}x^3+x^4+\dfrac{3}{8}\right)+\left(y-2013\right)^2=3x^4+\dfrac{1}{8}+\left(y-2013\right)^2\ge\dfrac{1}{8}\).
Dấu "=" xảy ra khi x = 0; y = 2013.
27 tháng 10 2024
đây là những món quà mà bn sẽ nhận đc: 1: áo quần 2: tiền 3: đc nhiều người yêu quý 4: may mắn cả 5: luôn vui vẻ trong cuộc sống 6: đc crush thích thầm 7: học giỏi 8: trở nên xinh đẹp phật sẽ ban cho bn những điều này nếu cậu gửi tin nhắn này cho 25 người,
17 tháng 12 2023
Bài 1:
a: \(M=x^2-10x+3\)
\(=x^2-10x+25-22\)
\(=\left(x^2-10x+25\right)-22\)
\(=\left(x-5\right)^2-22>=-22\forall x\)
Dấu '=' xảy ra khi x-5=0
=>x=5
b: \(N=x^2-x+2\)
\(=x^2-x+\dfrac{1}{4}+\dfrac{7}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{7}{4}>=\dfrac{7}{4}\forall x\)
Dấu '=' xảy ra khi x-1/2=0
=>x=1/2
c: \(P=3x^2-12x\)
\(=3\left(x^2-4x\right)\)
\(=3\left(x^2-4x+4-4\right)\)
\(=3\left(x-2\right)^2-12>=-12\forall x\)
Dấu '=' xảy ra khi x-2=0
=>x=2
6 tháng 10 2021
\(a,f\left(x\right)⋮g\left(x\right)\\ \Leftrightarrow\dfrac{-x^4+2x^2-3x+5}{x-1}\in Z\\ \Leftrightarrow\dfrac{-x^4+x^3-x^3+x^2+x^2-x-2x+2+3}{x-1}\in Z\\ \Leftrightarrow\dfrac{-x^3\left(x-1\right)-x^2\left(x-1\right)+x\left(x-1\right)-2\left(x-1\right)+3}{x-1}\in Z\\ \Leftrightarrow-x^3-x^2+x-2+\dfrac{3}{x-1}\in Z\\ \Leftrightarrow3⋮x-1\\ \Leftrightarrow x-1\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\\ \Leftrightarrow x\in\left\{-2;0;2;4\right\}\\ Mà.x< 0\\ \Leftrightarrow x=-2\\ b,B=\left(x^2-2xy+y^2\right)+4\left(x-y\right)+4+4y^2-2024\\ B=\left(x-y\right)^2+4\left(x-y\right)+4+4y^2-2024\\ B=\left(x-y-2\right)^2+4y^2-2024\ge-2024\\ B_{min}=-2024\Leftrightarrow\left\{{}\begin{matrix}x=y+2\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=0\end{matrix}\right.\)
CM
8 tháng 7 2017
Đáp án C
Ta có: y ' = 4 x 3 − 4 x = 0 ⇔ 4 x x 2 − 1 = 0 ⇔ x = 0 x = ± 1
Mà y 0 = 3 ; y 1 = 2 ; y 2 = 11 ⇒ M = 11 , m = 2.
30 tháng 8 2021
a) \(A=x^2-4x+1=\left(x-2\right)^2-3\ge-3\)
\(minA=-3\Leftrightarrow x=2\)
b) \(B=-x^2-8x+5=-\left(x+4\right)^2+21\le21\)
\(maxB=21\Leftrightarrow x=-4\)
c) \(C=2x^2-8x+19=2\left(x-2\right)^2+11\ge11\)
\(minC=11\Leftrightarrow x=2\)
d) \(D=-3x^2-6x+1=-3\left(x+1\right)^2+4\le4\)
\(maxD=4\Leftrightarrow x=-1\)
1
29 tháng 11 2023
\(B=\dfrac{x^4+2016x^2+4028}{x^2+2}\)
\(=\dfrac{x^4+2x^2+2014x^2+4028}{x^2+2}\)
\(=x^2+2014>=2014\forall x\)
Dấu '=' xảy ra khi x=0
9 tháng 7 2021
Bài 3:
a) Ta có: \(A=25x^2-20x+7\)
\(=\left(5x\right)^2-2\cdot5x\cdot2+4+3\)
\(=\left(5x-2\right)^2+3>0\forall x\)(đpcm)
d) Ta có: \(D=x^2-2x+2\)
\(=x^2-2x+1+1\)
\(=\left(x-1\right)^2+1>0\forall x\)(đpcm)
9 tháng 7 2021
Bài 1:
a) Ta có: \(A=x^2-2x+5\)
\(=x^2-2x+1+4\)
\(=\left(x-1\right)^2+4\ge4\forall x\)
Dấu '=' xảy ra khi x=1
b) Ta có: \(B=x^2-x+1\)
\(=x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)
CM
25 tháng 9 2019
Đặt 
Khi đó hàm số trở thành y= t2- 3t+1 với t≥ 1.
Bảng biến thiên
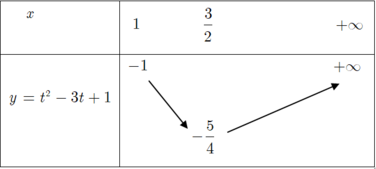
Suy ra giá trị nhỏ nhất của hàm số:
khi và chỉ khi t= 3/2 hay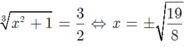 
Chọn C.
NT
1
20 tháng 4 2022
\(A=x^4+2x^2-8x+2019\) \(=x^4-2x^2+1+4x^2-8x+4+2014\)
\(=\left(x^2-1\right)^2+4\left(x-1\right)^2+2014\ge2014\forall x\)
" = " \(\Leftrightarrow x=1\)
F = x4 - 2x2 + 3 = x4 - 2x2 + 1 + 2 = (x2 - 1)2 + 2 \(\ge2\)
=> Min F = 2
Dấu "=" xảy ra <=> x2 - 1 = 0
<=> x = \(\pm1\)
Vậy Min F = 2 <=> x = \(\pm1\)
Ta có G = (x2 + 2)2 - 3
= x4 + 4x2 + 1 = x2(x2 + 4) + 1 \(\ge1\)
=> Min G = 1
Dấu "=" xảy ra <=> x2(x2 + 4) = 0
<=> x = 0
Vậy Min G = 1 <=> x = 0