Giải phương trình nghiệm nguyên \(x^2y-xy+2x-1=y^2-xy^2-2y\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


>>>>x^2-(2y^2+1-y)x+2y^2-y-1=0
>>>>delta=(2y^2+1-y)^2-4(2y^2-y-1) (tự tính nha bn)
có kq>>>để pt có no nguyên>>>>delta là sôc chính phương>>>xong

\(x^2-2y^2-xy+2x-y-2=0\)
\(\Leftrightarrow x^2+xy+x-2xy-2y^2-2y+x+y+1=3\)
\(\Leftrightarrow\left(x+y+1\right)\left(x-2y+1\right)=3\)
Mà \(x,y\)nguyên nên \(x+y+1,x-2y+1\)là các ước của \(3\).
Ta có bảng giá trị:
| x+y+1 | -3 | -1 | 1 | 3 |
| x-2y+1 | -1 | -3 | 3 | 1 |
| x | -10/3 (l) | -8/3 (l) | 2/3 (l) | 4/3 (l) |
| y |
Vậy phương trình đã cho không có nghiệm nguyên.



b) x2y + x + xy2 + y + 2xy = 9
xy(x + y + 2) + (x + y + 2) = 11
<=> (xy + 1)(x + y + 2) = 11
Xét các TH
+) \(\hept{\begin{cases}xy+1=1\\x+y+2=11\end{cases}}\) <=> \(\hept{\begin{cases}xy=0\\x+y=9\end{cases}}\) <=> x = 0 => y = 9 hoặc y = 0 => x = 9
+) \(\hept{\begin{cases}xy+1=-1\\x+y+2=-11\end{cases}}\)<=> \(\hept{\begin{cases}xy=-2\\x+y=-13\end{cases}}\) <=> \(\hept{\begin{cases}x=-13-y\\y\left(-13-y\right)=-2\end{cases}}\)
<=> \(\hept{\begin{cases}x=-13-y\\y^2+13y-2=0\end{cases}}\)(loại)
+) \(\hept{\begin{cases}xy+1=11\\x+y+2=1\end{cases}}\) <=> \(\hept{\begin{cases}xy=10\\x+y=-1\end{cases}}\) <=> \(\hept{\begin{cases}y\left(-1-y\right)=10\\x=-1-y\end{cases}}\) <=> \(\hept{\begin{cases}y^2+y+10=0\\x=-1-y\end{cases}}\)(loại)
+) \(\hept{\begin{cases}xy+1=-11\\x+y+2=-1\end{cases}}\) <=> \(\hept{\begin{cases}xy=-12\\x+y=-3\end{cases}}\) <=> \(\hept{\begin{cases}y\left(-3-y\right)=-12\\x=-3-y\end{cases}}\) <=> \(\hept{\begin{cases}y^2+3y-12=0\\x=-3-y\end{cases}}\) (loại)

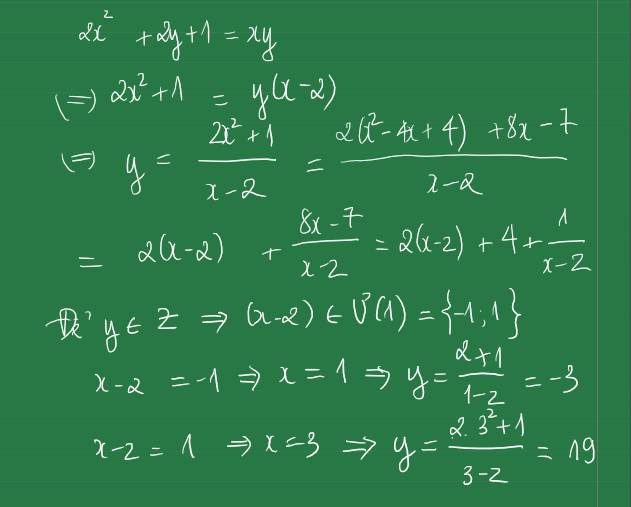
Ta có x2y - xy + 2x - 1 = y2 - xy2 - 2y
<=> x2y - xy + 2x - y2 + xy2 + 2y = 1
<=> xy(x + y) - y(x + y) + 2(x + y) = 1
<=> (x + y)(xy - y + 2) = 1
Lập bảng xét các trường hợp
Khi x + y = 1 và xy - y + 2 = -1
=> các cặp (x;y) thỏa là : (0;1) ; (2;-1)
Khi x + y = -1 và xy - y + 2 = -1
=> các cặp (x;y) thỏa là (-2 ; 1) ; (2 ; - 3)
Vậy các cặp (x;y) nguyên thỏa mãn là (0;1) ; (2; - 1) ; (-2; 1) ; (2; -3)
\(x^2y-xy+2x-1=y^2-xy^2-2y\)
\(\Leftrightarrow x^2y+xy^2-xy-y^2+2x+2y=1\)
\(\Leftrightarrow xy\left(x+y\right)-y\left(x+y\right)+2\left(x+y\right)=1\)
\(\Leftrightarrow\left(x+y\right)\left(xy-y+2\right)=1\)
vì \(x,y\)nguyên nên \(x+y,xy-y+2\)là ước của \(1\).
- Với \(\hept{\begin{cases}x+y=1\\xy-y+2=1\end{cases}}\Rightarrow y\left(1-y\right)-y+2=1\)
\(\Leftrightarrow\hept{\begin{cases}y=1\Rightarrow x=0\\y=-1\Rightarrow x=2\end{cases}}\)(thỏa)
- Với \(\hept{\begin{cases}x+y=-1\\xy-y+2=-1\end{cases}}\Rightarrow y\left(-1-y\right)-y+2=-1\)
\(\Leftrightarrow\hept{\begin{cases}y=1\Rightarrow x=-2\\y=-3\Rightarrow x=2\end{cases}}\)(thỏa)