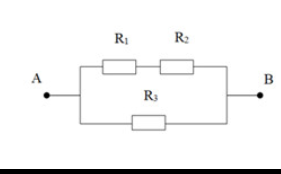
Cho mạch điện như hình vẽ R1 = 4 R2 = 6 R3 = 3 UAB = 9V không đổi a) Tính điện trở tương đương của đoạn mạch. b) Tính cường độ dòng điện qua mỗi điện trở. c) Thay R1 bởi điện trở Rx sao cho cường độ dòng điện qua mạch giảm 3 lần. Tính Rx.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 7 2021
a,\(R1nt\left(R2//R3\right)=>Rtd=R1+\dfrac{R2R3}{R2+R3}=4+\dfrac{6.3}{6+3}=6\left(om\right)\)
b,\(=>I1=I23=\dfrac{Uab}{Rtd}=\dfrac{9}{6}=1,5A\)
\(=>U23=I23.R23=1,5.\dfrac{6.3}{6+3}=3V=U2=U3\)
\(=>I2=\dfrac{U2}{R2}=\dfrac{3}{6}=0,5A,=>I3=\dfrac{U3}{R3}=\dfrac{3}{3}=1A\)
c,\(=>Im=Ix=I23=\dfrac{1}{3}.1,5=0,5A\)
\(=>RTd=Rx+\dfrac{R2.R3}{R2+R3}=Rx+\dfrac{6.3}{6+3}=\dfrac{U}{Im}=\dfrac{9}{0,5}=18\)
\(=>Rx=16\left(om\right)\)
N
15 tháng 10 2021
Điện trở tương đương: \(R=\dfrac{\left(R1+R2\right)R3}{R1+R2+R3}=\dfrac{\left(15+25\right)10}{15+25+10}=8\Omega\)
\(U=U12=U3=12V\)(R12//R3)
\(I=U:R=12:8=1,5A\)
\(I3=U3:R3=12:10=1,2A\)
\(R1ntR2\Rightarrow I12=I1=I2\)
Mà: \(I12=I-I3=1,5-1,2=0,3A\)
\(\Rightarrow I12=I1=I2=0,3A\)
NT
5 tháng 9 2021
a. Vì \(R_1ntR_2\) nên \(R_{12}=R_1+R_2=15+25=40\left(\text{Ω}\right)\)
Vì \(R_{12}//R_3\) nên \(\dfrac{1}{R_{td}}=\dfrac{1}{R_{12}}+\dfrac{1}{R_3}\Rightarrow R_{td}=\dfrac{R_{12}.R_3}{R_{12}+R_3}=\dfrac{40.10}{40+10}=8\left(\text{Ω}\right)\)
b. Ta có \(I=\dfrac{U}{R_{td}}=\dfrac{12}{8}=1,5\left(A\right)\)
mà \(U_{12}=U_3\Leftrightarrow R_{12}.I_{12}=R_3.I_3\Leftrightarrow40I_{12}=10I_3\Leftrightarrow I_3=4I_{12}\) (1)
mặt khác, ta có \(I=I_{12}+I_3\) (2)
Từ (1) và (2) \(\Rightarrow I_{12}+4I_{12}=1,5\Rightarrow I_{12}=0,3\left(A\right)\)
\(\Rightarrow I_3=I-I_{12}=1,5-0,3=1,2\left(A\right)\)
c. Ta có \(R_{td'}=\dfrac{R_{2x}.R_3}{R_{2x}+R_3}=\dfrac{\left(25+R_x\right)10}{R_x+25+10}=\dfrac{250+10R_x}{35+R_x}=7,5\left(\text{Ω}\right)\)
\(\Rightarrow R_x=5\left(\text{Ω}\right)\)
NT
5 tháng 9 2021
Bạn chụp thêm hình vẽ nữa chứ không biết mắc song song hay nối tiếp để làm
7 tháng 10 2021
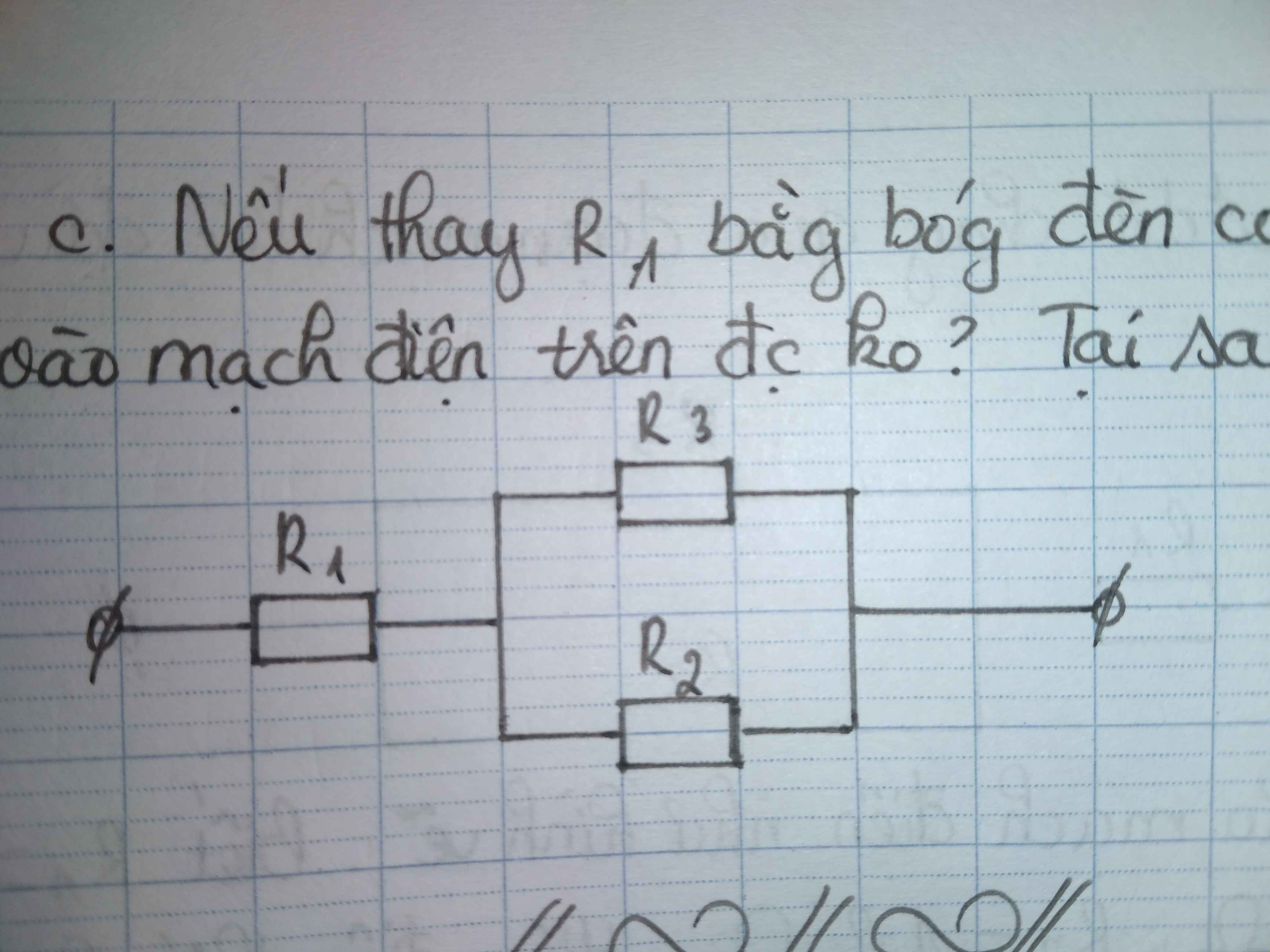
\(\Rightarrow\left\{{}\begin{matrix}a,R1//\left(R2ntR3\right)\Rightarrow Rtd=\dfrac{R1\left(R2+R3\right)}{R1+R2+R3}=6\Omega\\b,\Rightarrow\left\{{}\begin{matrix}U=U1=U23=24V\Rightarrow I1=\dfrac{U1}{R1}=\dfrac{8}{3}A\\I2=I3=\dfrac{U23}{R2+R3}=\dfrac{4}{3}A\\U2=I2.R2=8V\\U3=U-U2=16V\end{matrix}\right.\\c,R1//\left(R2ntRx\right)\Rightarrow Im=1,5.\dfrac{24}{6}=6A\\\Rightarrow Rtd=\dfrac{R1\left(R2+Rx\right)}{R1+R2+Rx}=\dfrac{9\left(6+Rx\right)}{15+Rx}=\dfrac{24}{Im}=4\left(\Omega\right)\Rightarrow Rx=1,2\Omega\end{matrix}\right.\)
N
15 tháng 10 2021
Điện trở: \(R=R1+\left(\dfrac{R2.R3}{R2+R3}\right)=16+\left(\dfrac{24.12}{24+12}\right)=24\Omega\)
Cường độ dòng điện R, R1 và R23:
\(\left\{{}\begin{matrix}I=U:R=24:24=1A\\I=I1=I23=1A\left(R1ntR23\right)\end{matrix}\right.\)
Hiệu điện thế R1 VÀ R23:
\(\left\{{}\begin{matrix}U1=R1.I1=16.1=16V\\U23=U-U1=24-16=8V\end{matrix}\right.\)
\(\Rightarrow U23=U2=U3=8V\)(R1//R23)
\(\left\{{}\begin{matrix}I2=U2:R2=8:24=\dfrac{1}{3}A\\I3=U3:R3=8:12=\dfrac{2}{3}A\end{matrix}\right.\)
30 tháng 9 2023
\(R_{12}=\dfrac{15.30}{15+30}=10\left(\Omega\right)\)
\(R_m=R_{12}+R_3=10+30=40\left(\Omega\right)\)
\(I_m=\dfrac{U_{AB}}{R_m}=\dfrac{12}{40}=0,3\left(A\right)\)
\(b,I_{12}=I_3=0,3\left(A\right)\)
\(\dfrac{I_1}{I_2}=\dfrac{R_2}{R_1}=\dfrac{30}{15}=\dfrac{2}{1}\)
\(\rightarrow I_1=0,2\left(A\right);I_2=0,1\left(A\right)\)
Hình đâu bạn?
hình đâu chẳng thấy toàn hình bóng e haha