Cho A4=120°
B1=60°
Chứng tỏ a//b (3 cách)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TT
1
Những câu hỏi liên quan
NT
1
14 tháng 9 2019
Tham khảo : Câu hỏi của huy nguyễn - Toán lớp 7 - Học toán với OnlineMath
26 tháng 8 2019
a A 3 2 4 1 c b B 3 2 4 1
a, \(\widehat{B}_1=\widehat{B_3}\) đối đỉnh
\(\widehat{A}_1=\widehat{B}_1\) theo bài đầu
Do đó \(\widehat{A_1}=\widehat{B_3}\)
Mặt khác,ta có \(\widehat{A_1}+\widehat{A_4}=180^0\) hai góc kề bù
=> \(\widehat{A_4}=180^0-\widehat{A_1}\) \((1)\)
Và \(\widehat{B_2}+\widehat{B_3}=180^0\) hai góc kề bù
=> \(\widehat{B_2}=180^0-\widehat{B_3}\) \((2)\)
\(\widehat{A_1}=\widehat{B_3}\) \((3)\)
Từ 1,2,3 ta có : \(\widehat{A_4}=\widehat{B_2}\)
b, \(\widehat{A_2}=\widehat{A_4}\) đối đỉnh
\(\widehat{A_4}=\widehat{B_2}\) theo câu a
Do đó : \(\widehat{A_2}=\widehat{B_2};\widehat{A_1}=\widehat{A_3}\) đối đỉnh
\(\widehat{A_1}=\widehat{B_3}\) câu a
Do đó \(\widehat{A_3}=\widehat{B_3}\). Mặt khác \(\widehat{B_2}=\widehat{B_4}\) hai góc đối đỉnh
\(\widehat{A_4}=\widehat{B_2}\) câu a . Do đó \(\widehat{A_4}=\widehat{B_4}\)
c, \(\widehat{B_1}+\widehat{B_2}=180^0\) hai góc kề bù
\(\widehat{A_1}=\widehat{B_1}\) theo đầu bài
Do đó \(\widehat{A_1}+\widehat{B_2}=180^0\)
Mặt khác \(\widehat{B_2}+\widehat{B_3}=180^0\) kề bù
\(\widehat{A_4}=\widehat{B_2}\) theo câu a . Do đó \(\widehat{A_4}+\widehat{B_3}=180^0\)
CM
6 tháng 8 2019
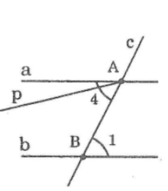
Nếu ∠(A4) ≠ ∠(B1 ) thì qua A ta vẽ tia Ap sao cho ∠(pAB) = ∠(B1)
Vì đường thẳng c cắt hai đường thẳng Ap và b và trong các góc tạo thành có cặp góc so le trong bằng nhau là: ∠(pAB) = ∠(B1). Do đó, Ap // b ( tính chất hai đường thẳng song song)
Khi đó, qua A, ta có hai đường thẳng a và Ap cùng song song với đường thẳng b (trái với tiên đề Ơ clit về đường thẳng song song).
Kết luận: đường thẳng Ap và đường thẳng a chỉ là một. Nói cách khác, ∠(pAB) = ∠(A4 ) ,từ đó ∠(A4 ) = ∠(B1)
TD
5
DV
23 tháng 10 2017
Ta có : \(B_2+B_3=180^o\) ( 2 góc kề bù )
Mà : \(B_3=120^o\left(gt\right)\)
\(\Rightarrow B_2+120^o=180^o\Rightarrow B_2=60^o\)
\(\Rightarrow B_2=A_4\left(=60^o\right)\) ( 2 góc so le trong )
=> a // b ( t/c 2 đg thẳng // )
Vậy ...
23 tháng 10 2017
Vì góc B2 và B3 là hai góc kề bù
=> B2 + B3=180o
=> 120o + B2 = 180o
=> B2 = 180o - 120o = 60o
=>B2 = A4 mà hai góc ở vị trí so le trong
=> a // b
27 tháng 12 2020
Mình làm được b1 thôi nha
A=2+2²+2³+...+2^60
2A=2(2+2²+2³+...+2^60)
2A=2²+2³+2⁴+...+2^61
2A-A=(2²+2³+2⁴+...+2^61)-(2+2²+2³+...+2^60)
A=2^61-2
Vậy A=2^61-2
\(=>\angle\left(A1\right)=180^o-\angle\left(A4\right)=60^o=\angle\left(B1\right)\)
2 góc này ở vt so le trong nên a//b
c2.
\(=>\angle\left(B2\right)=180^o-\angle\left(B1\right)=120^o=\angle\left(A4\right)\)
2 góc ở vt đồng vị =>a//b
c3
giống 2 cách trên để tính ra \(\angle\left(A1\right)=60^o,\angle\left(B2\right)=120^0=>\angle\left(A1\right)+\angle\left(B2\right)=180^0\)
2 góc ở vt trong cùng phía=>a//b