K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LT
0
ST
1
NN
13 tháng 4 2021
Hmm, nói đến cờ chắc là dấu hiệu của semaphore, thử mò xem :v
MH
30 tháng 3 2022
a) \(\left|7x-4\right|=-7\)
Mà \(\left|7x-4\right|\ge0\forall x\)
\(\Rightarrow\) phương trình vô nghiệm
b) \(\left|3x-4\right|=\left|7x+5\right|\)
\(\Rightarrow\left[{}\begin{matrix}3x-4=7x+5\\3x-4=-7x-5\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{9}{4}\\x=-\dfrac{1}{10}\end{matrix}\right.\)
Vậy ...
TV
0
NL
0
LT
0
HV
1
19 tháng 12 2023
a: \(VP=a^3+b^3+c^3-3bac\)
\(=\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc\)
\(=\left(a+b+c\right)\left[\left(a+b\right)^2-c\left(a+b\right)+c^2\right]-3ab\left(a+b+c\right)\)
\(=\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2-3ab\right)\)
\(=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ac\right)=VT\)
b: \(VT=\left(3a+2b-1\right)\left(a+5\right)-2b\left(a-2\right)\)
\(=3a^2+15a+2ab+10b-a-5-2ab+4b\)
\(=3a^2+14a+14b-5\)
\(VP=\left(3a+5\right)\left(a+3\right)+2\left(7b-10\right)\)
\(=3a^2+9a+5a+15+14b-20\)
\(=3a^2+14a+14b-5\)
=>VT=VP
c: \(VT=a\left(b-x\right)+x\left(a+b\right)\)
\(=ab-ax+ax+bx\)
\(=ab+bx=b\left(a+x\right)=VP\)
d: \(VT=a\left(b-c\right)-b\left(a+c\right)+c\left(a-b\right)\)
\(=ab-ac-ab-bc+ca-cb\)
\(=-2bc\)
=VP
QA
1
GL
5 tháng 8 2023
B1
1. is
2. is
3. are
4. is
5. is/ am
6. aren't
7. are
8. Is she
9. is
10. are
B2
5. doesn't
7. don't
8. doesn't
9. don't
10. don't
B3
1. starts
2. likes
3. bake
4. writes
5. doesn't know
6. has
7. swim
8. helps
-----------
CT thì hiện tại đơn:
(+) S + V(s/es) + O
(-) S + don't/ doesn't + V + O
(?) Do/Does + S + V + O?
Tobe: am/is/are
- Nếu chủ ngữ là số ít, he, she, it thì tobe là is và V phải thêm s/es.
- Nếu chủ ngữ là số nhiều, you, we, they thì to be là are và V giữ nguyên.
- Nếu chủ ngữ là I thì tobe là am và V cũng giữ nguyên.
DT
1
29 tháng 12 2021
Câu 5:
\(\Leftrightarrow-x^2+7x-9+2x-9=0\)
\(\Leftrightarrow x^2-9x+18=0\)
=>x=3
=>Chọn A
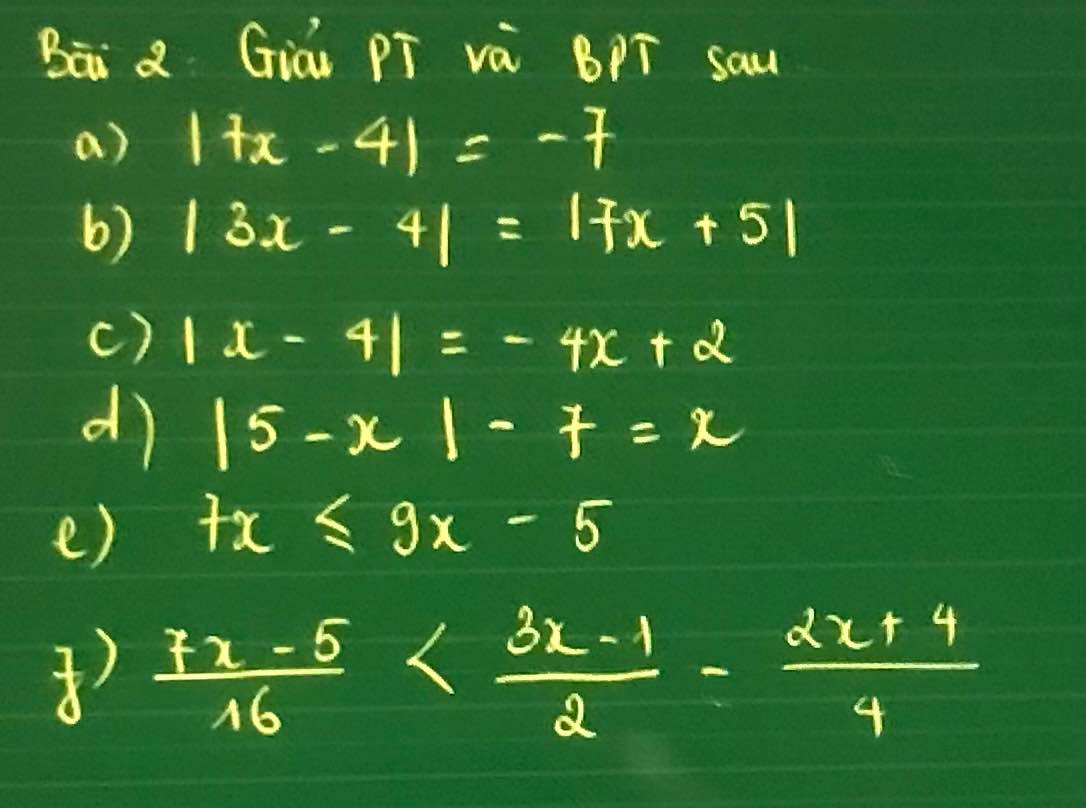
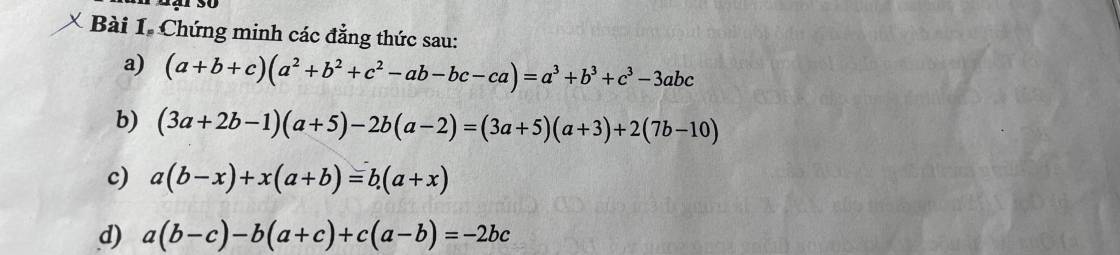
A B C H D 20cm 15cm
Hình vẽ chỉ mang tính chất minh họa
a, Xét tam giác ABC và tam giác HBA có :
\(\hept{\begin{cases}\widehat{A}=\widehat{H}=90^o\\\widehat{B}:chung\end{cases}}\)
=>Tam giác ABC đồng dạng với tam giác HBA(g.g)
b, Áp dụng định lí Py-ta-go vào tam giác ABC vuông tại A, ta có:
BC=\(\sqrt{AB^2+AC^2}\)
BC=\(\sqrt{20^2+15^2}\)
BC=25(cm)
Lại có: Stam giác ABC=\(\frac{1}{2}AB.AC=\frac{1}{2}BC.AH\)
=> AB.AC=BC.AH
=>AH=\(\frac{AB.AC}{BC}\)
=>AH=\(\frac{20.15}{25}=12\)(cm)
Áp dụng định lí Py-ta-go vào tam giác HAB vuông tại H, ta có:
=> BH=\(\sqrt{AB^2-AH^2}\)
=> BH=\(\sqrt{20^2-12^2}\)
=> BH=16(cm)
=> CH=BC-BH=25-16=9(cm)
c, Áp dụng tính chất tia phân giác, ta có:
\(\frac{DB}{DC}=\frac{AB}{AC}\)
=>\(\frac{DB}{DC+DB}=\frac{AB}{AC+AB}\)
=>\(\frac{DB}{25}=\frac{20}{15+20}\)
=>\(\frac{DB}{25}=\frac{20}{35}\)
=>\(DB=\frac{20.25}{35}=\frac{100}{7}\)(cm)
=> HD=BH-BD=\(16-\frac{100}{7}=\frac{12}{7}\)(cm)
Tam giác AHD vuông tại H
=>Stam giác AHD=\(\frac{1}{2}AH.HD=\frac{1}{2}.12.\frac{12}{7}=\frac{72}{7}\)(cm2)