Cho tam giác ABC vuông tại A. Lấy M là1 điểm bất kỳ thuộc cạnh BC. Gọi MD là đường vuông góc kẻ từ M đến AB, ME là đường vuông góc kẻ từ M đến AC, O là trung điểm của DE
a) CM: 3 điểm A,O,M thẳng hàng
b) Khi điểm M di chuyển trên cạnh BC thì điểm O di chuyển trên đường nào?
c)Điểm M ở vị trí nào trên cạnh BC thì điểm AM có độ dài nhỏ nhất?

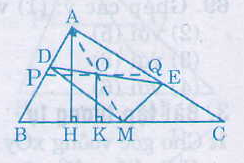
Bạn chỉ cần chứng minh AEDM là HCN ;O là trung điểm của DE =>O cũng là trung điểm của AM =>O,M,A thẳng hàng
b,
Gọi P ,Q lần lượt là trung điểm của AB,AC
=> giới hạn :
*Khi M trùng với B=> O trùng với P
*Khi M trùng với C=> O trùng với Q
=> I thuộc PQ
c,
Kẻ đường cao AH
Khi M trùng với H thì AM ngắn nhất (quan hệ đường vuông góc và đường xiên)