Tìm các giá trị nguyên của x để :(x2 - x - 1) ⋮ (x -...
Đọc tiếp
Tìm các giá trị nguyên của x để :
(x2 - x - 1) ⋮ (x - 1)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 3 2021
đề bài ĐKXĐ như nào bạn tự xét gtri thỏa mãn nhé
\(P=\frac{x^2}{x-1}=\frac{x^2-x+x-1+1}{x-1}=\frac{x\left(x-1\right)+\left(x-1\right)+1}{x-1}=x+1+\frac{1}{x-1}\)
Vì x nguyên nên x + 1 nguyên
Để P nguyên thì 1/x-1 nguyên ( đến đây quá dễ rồi:)) )
Như trên ta có : \(P=x+1+\frac{1}{x-1}=\left[\left(x-1\right)+\frac{1}{x-1}\right]+2\)
Vì x > 1, áp dụng bất đẳng thức AM-GM ta có :
\(P\ge2\sqrt{\left(x-1\right)\cdot\frac{1}{x-1}}+2=4\). Đẳng thức xảy ra <=> x = 2
Vậy GTNN của P = 4 <=> x=2
27 tháng 7 2021
Bài 1:
a) Ta có: \(P=1+\dfrac{3}{x^2+5x+6}:\left(\dfrac{8x^2}{4x^3-8x^2}-\dfrac{3x}{3x^2-12}-\dfrac{1}{x+2}\right)\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}:\left(\dfrac{8x^2}{4x^2\left(x-2\right)}-\dfrac{3x}{3\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x+2}\right)\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}:\left(\dfrac{4}{x-2}-\dfrac{x}{\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x+2}\right)\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}:\dfrac{4\left(x+2\right)-x-\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}\cdot\dfrac{\left(x-2\right)\left(x+2\right)}{4x+8-x-x+2}\)
\(=1+3\cdot\dfrac{\left(x-2\right)}{\left(x+3\right)\left(2x+10\right)}\)
\(=1+\dfrac{3\left(x-2\right)}{\left(x+3\right)\left(2x+10\right)}\)
\(=\dfrac{\left(x+3\right)\left(2x+10\right)+3\left(x-2\right)}{\left(x+3\right)\left(2x+10\right)}\)
\(=\dfrac{2x^2+10x+6x+30+3x-6}{\left(x+3\right)\left(2x+10\right)}\)
\(=\dfrac{2x^2+19x-6}{\left(x+3\right)\left(2x+10\right)}\)
CM
27 tháng 9 2018
c) Để A nhận giá trị nguyên khi và chỉ khi:
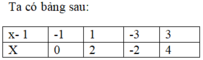
Kết hợp với điều kiện, tập hợp các giá trị của x nguyên để A nguyên là: {0; 2; -2; 4}.
29 tháng 7 2023
a: \(P=\dfrac{x^2-x-18+2x+6-4x+12}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{x^2-3x}{\left(x-3\right)\left(x+3\right)}=\dfrac{x}{x+3}\)
b: P=2/3
=>x/(x+3)=2/3
=>3x=2x+6
=>x=6(nhận)
c: P nguyên
=>x chia hết cho x+3
=>x+3-3 chia hết cho x+3
=>x+3 thuộc {1;-1;2;-2}
=>x thuộc {-2;-4;-1;-5}
KN
0
PT
1
CM
16 tháng 8 2018
Hướng dẫn giải:
Điều kiện xác định của phân thức: x ≠ 1
Ta có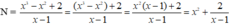 
Để N nguyên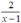 
nguyên ⇒ x - 1 là ước của 2
Ư ( 2 ) = 1 ; - 1 ; 2 ; - 2
x – 1 = 1 ⇒ x =2 (thỏa mãn điều kiện xác định);
x - 1 = -1 ⇒ x = 0 (thỏa mãn điều kiện xác định);
x - 1 = 2 ⇒ x = 3 (thỏa mãn điều kiện xác định);
x - 1 = -2 ⇒ x = -1 (thỏa mãn điều kiện xác định);
Vậy với x ∈ { -1;0;2;3 } thì phân thức N nhận giá trị nguyên
TN
19 tháng 5 2021
a) Ta có: \(M=\dfrac{8x+1}{4x-5}=\dfrac{8x-10+11}{4x-5}=\dfrac{2\left(x-5\right)+11}{4x-5}=2+\dfrac{11}{4x-5}\)
Để M nhận giá trị nguyên thì \(2+\dfrac{11}{4x-5}\) nhận giá trị nguyên
\(\Rightarrow\dfrac{11}{4x-5}\) nhận giá trị nguyên
\(\Rightarrow11⋮4x-5\)
Vì \(x\in Z\) nên \(4x-5\in Z\)
\(\Rightarrow4x-5\inƯ\left(11\right)=\left\{\pm1;\pm11\right\}\)
\(\Rightarrow x\in\left\{1;\pm1,5;4\right\}\)
Vậy \(x\in\left\{1;4\right\}\) thỏa mãn \(x\in Z\).
b) Ta có: \(A=\dfrac{5}{4-x}\). ĐK: \(x\ne4\)
Nếu 4 - x < 0 thì x > 4 \(\Rightarrow A>0\)
4 - x > 0 thì x < 4 \(\Rightarrow A< 0\)
Để A đạt GTLN thì 4 - x là số nguyên dương nhỏ nhất
\(\Rightarrow4-x=1\Rightarrow x=3\)
\(\Rightarrow A=\dfrac{5}{4-3}=5\)
Vậy MaxA = 5 tại x = 3
c) \(B=\dfrac{8-x}{x-3}\). ĐK: \(x\ne3\).
Ta có: \(B=\dfrac{8-x}{x-3}=\dfrac{-\left(x-8\right)}{x-3}=\dfrac{-\left(x-3\right)+5}{x-3}=\dfrac{5}{x-3}-1\)
Để B đạt giá trị nhỏ nhất thì \(\dfrac{5}{x-3}-1\) nhỏ nhất
\(\Rightarrow\dfrac{5}{x-3}\) nhỏ nhất
Nếu x - 3 > 0 thì x > 3 \(\Rightarrow\dfrac{5}{x-3}>0\)
x - 3 < 0 thì x < 3 \(\Rightarrow\dfrac{5}{x-3}< 0\)
Để \(\dfrac{5}{x-3}\) nhỏ nhất thì x - 3 là số nguyên âm lớn nhất
\(\Rightarrow x-3=-1\Rightarrow x=2\)
\(\Rightarrow B=\dfrac{8-2}{2-3}=-6\)
Vậy MaxB = -6 tại x = 2.
TN
19 tháng 5 2021
Mình làm sai câu a...
Ta có: \(M=\dfrac{8x+1}{4x-1}=\dfrac{8x-2+3}{4x-1}=\dfrac{2\left(4x-1\right)+3}{4x-1}=2+\dfrac{3}{4x-1}\)
Để M nhận giá trị nguyên thì \(2+\dfrac{3}{4x-1}\) nhận giá trị nguyên
\(\Rightarrow\dfrac{3}{4x-1}\) nhận giá trị nguyên
Vì \(4x-1\in Z\) nên \(4x-1\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
\(\Rightarrow x\in\left\{\pm0,5;0;1\right\}\)
Vậy \(x\in\left\{0;1\right\}\) thỏa mãn \(x\in Z\).
\(\left(x^2-x-1\right)⋮\left(x-1\right)\Rightarrow[x\left(x-1\right)-1]⋮\)(x-1) mà x(x-1) chia hết cho x-1 suy ra 1 chia hết x-1 suy ra x-1 thuộc ư(1) suy ra x-1 thuộc (1;-1)suy ra x thuộc (2;0)
\(\left(x^2-x-1\right)⋮\left(x-1\right)\)
\(\Rightarrow\left(x^2-2x+1+x-2\right)⋮\left(x-1\right)\)
\(\Rightarrow\left[\left(x-1\right)^2+x-2\right]⋮\left(x-1\right)\)
Vì \(\left(x-1\right)^2⋮\left(x-1\right)\)nên \(\left(x-2\right)⋮\left(x-1\right)\)
\(\Rightarrow\left(x-1-1\right)⋮\left(x-1\right)\)
Vì \(\left(x-1\right)⋮\left(x-1\right)\)nên \(-1⋮\left(x-1\right)\)\(\Rightarrow\left(x-1\right)\inƯ\left(-1\right)\)
\(\Rightarrow x\in\left(0;2\right)\)