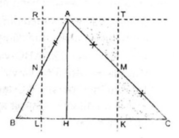
Dựa vào công thức tính diện tích của đa giác đều để chứng minh công thức tính diện tích hình tròn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


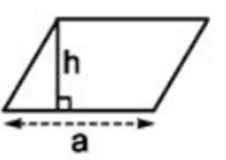
Hình bình hành là hình thang có hai đáy bằng nhau
⇒ Hình bình hành có cạnh đáy a và chiều cao h là:
S = 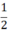 h(a + a) =
h(a + a) = 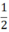 h.2a = a.h
h.2a = a.h

Xét △ ABC. Kẻ đường cao AH. Gọi M là trung điểm của AC, N là trung điểm của AB.
Từ M kẻ đường thẳng song song AH cắt BC tại K
Từ N kẻ đường thẳng song song AH cắt BC tại L
Từ A kẻ đường thẳng song song BC cắt hai đường thẳng MK và NL tại T và R
Ta có: △ MKC = △ MTA
△ NLB = △ NAR
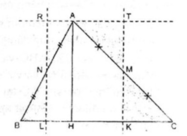
Cắt △ ABC theo đường MK và NL ta ghép lại được một hình chữ nhật KTRL có diện tích bằng diện tích tam giác ABC

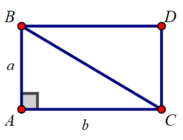
Muốn tính diện tích tam giác vuông ABC, ta dựng hình chữ nhật ABDC như trên
- ∆ABC = ∆DCB (hai cạnh góc vuông)
⇒SABC = SDCB (theo tính chất 1 diện tích đa giác) (1)
Đường chéo BC chia hình chữ nhật ABDC thành 2 phần là ∆ABC và ∆DCB
⇒SABDC = SABC + SDCB (theo tính chất 2 diện tích đa giác) (2)
Từ (1) và (2) ⇒ SABDC = 2SABC ⇒ SABC = 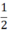 SABDC
SABDC
- ABDC là hình chữ nhật ⇒ SABDC = a.b
⇒ SABC = 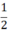 SABDC =
SABDC = 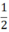 ab
ab

Trl :
* Toán :
Công thức tính diện tích Hình chữ nhật
Diện tích: S = a x b.
Công thức tính diện tích Hình vuông
S = a x a.
Biết DT tìm cạnh bằng cách nhẩm.
Công thức tính diện tích Hình tam giác
S = (a x h) : 2
Trong đó:
- a là cạnh đáy
- h : chiều cao
Chiều cao: h = (S x 2) : a
Cạnh đáy: a = (S x 2) : h
Công thức tính chu vi Hình tam giác
P = a + b + c
Trong đó:
- a là cạnh thứ nhất
- b là cạnh thứ hai
- c là cạnh thứ ba
Công thức tính diện tích Hình thoi
S = (a x b) : 2
Trong đó: a và b là số đo độ dài hai đường chéo.

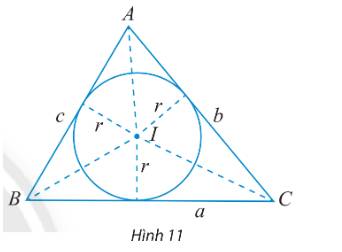
a) Diện tích \({S_1}\) của tam giác IAB là: \({S_1} = \frac{1}{2}r.AB = \frac{1}{2}r.c\)
Diện tích \({S_2}\) của tam giác IAC là: \({S_2} = \frac{1}{2}r.AC = \frac{1}{2}r.b\)
Diện tích \({S_3}\) của tam giác IBC là: \({S_3} = \frac{1}{2}r.BC = \frac{1}{2}r.a\)
b) Diện tích S của tam giác ABC là:
\(\begin{array}{l}S = {S_1} + {S_2} + {S_3} = \frac{1}{2}r.c + \frac{1}{2}r.b + \frac{1}{2}r.a = \frac{1}{2}r.(c + b + a)\\ \Leftrightarrow S = \frac{{r(a + b + c)}}{2}\end{array}\)

HÌNH CHỮ NHẬT
- Chu vi: P = (a + b) x 2 (P: chu vi)
- Diện tích: S = a x b (S: diện tích)
HÌNH VUÔNG:
- Chu vi: P = a x 4 (P: chu vi)
- Diện tích: S = a x a (S: diện tích)
HÌNH TAM GIÁC:
- Chu vi: P = a + b + c (a: cạnh thứ nhất; b: cạnh thứ hai; c: cạnh thứ ba)
- Diện tích: S = (a x h) : 2 (a: cạnh đáy)
- Chiều cao: h = (S x 2) : a (h: chiều cao)
- Cạnh đáy: a = (S x 2) : h
HÌNH BÌNH HÀNH:
- Chu vi: P = (a + b) x 2 (a: độ dài đáy)
- Diện tích: S = a x h (b: cạnh bên)
- Diện tích: S = a x h (h: chiều cao)
- Độ dài đáy: a = S : h
- Chiều cao: h = S : a
- Diện tích: S = (m x n) : 2 (m: đường chéo thứ nhất)
- Tích 2 đường chéo: (m x n) = S x 2 (n: đường chéo thứ nhất)
- HÌNH THANG
- Diện tích: S = (a + b) x h : 2 (a & b: cạnh đáy)
- Chiều cao: h = (S x 2) : a (h: chiều cao)
- Cạnh đáy: a = (S x 2) : h
HÌNH TRÒN:
- Bán kính hình tròn: r = d : 2 hoặc r = C : 2 : 3,14
- Đường kính hình tròn: d = r x 2 hoặc d = C : 3,14
- Chu vi hình tròn: C = r x 2 x 3,14 hoặc C = d x 3,14
- Diện tích hình tròn: C = r x r x 3,14
- Diện tích xung quanh: Sxq = (a x a) x 4
- Cạnh: (a x a) = Sxq : 4
- Diện tích toàn phần: Stp = (a x a) x 6
- Cạnh: (a x a) = Stp : 6
- Diện tích xung quanh: Sxq = Pđáy x h
- Chu vi đáy: Pđáy = Sxq : h
- Chiều cao: h = Pđáy x Sxq

a) Diện tích xung quanh hình lăng trụ thì bằng chu vi đường tròn đáy nhân với chiều cao.
b) Thể tích hình trụ thì bằng tích của diện tích hình tròn đáy nhân với đường cao.
c) Diện tích xung quanh hình nón thì bằng 1/2 tích của chu vi đường tròn đáy với đường sinh.
d) Thể tích hình nón bằng 1/3 tích của diện tích hình tròn đáy với chiều cao.
e) Diện tích mặt cầu thì bằng 4 lần diện tích hình tròn lớn.
f) Thể tích hình cầu thì bằng 4/3 tích của diện tích hình tròn lớn với bán kính.