Tại hai điểm A và B cách nhau một khoảng L trên một đường thẳng có ba xe cùng xuất phát và chuyển động thẳng đều. Xe 1 xuất phát từ A đi theo hướng AB, xe 2 xuất phát từ B đi cùng hướng xe 1, xe 3 xuất phát từ B đi theo hướng BA. Vận tốc của xe 1, xe 2, xe 3 lần lượt là v1 = 30km/h; v2 = 40km/h; v3 = 50km/h. Khi gặp xe 1 thì xe 3 lập tức quay lại đuổi theo xe 2. Thời gian từ lúc xe 3 gặp xe 1 đến lúc xe 3 đuổi kịp xe 2 là 5,4 phút. Coi vận tốc của mỗi xe là không đổi, bỏ qua thời gian xe quay đầu. a) Tính khoảng cách L và thời gian từ khi các xe xuất phát đến khi xe 3 gặp xe 1. b) Khi xe 3 đuổi kịp xe 2 thì xe 3 cách xe 1 một khoảng bao nhiêu?
BÀI 42. Trên đường thẳng có ba người: Người đi xe đạp, người đi xe máy và người đi bộ ở giữa hai người trên. Ban đầu khoảng cách từ người đi bộ tới người đi xe đạp nhỏ hơn hai lần so với khoảng cách từ người đi bộ tới người đi xe máy. Vận tốc của người đi xe đạp và người đi xe máy tương ứng là 20km/h và 60km/h. Người đi bộ cần đi theo hướng nào và với vận tốc bằng bao nhiêu để ba người cùng gặp nhau tại một điểm?

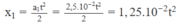

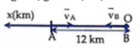
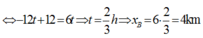
- Gọi thời gian xuất phát là to, điểm gốc tại A, chiều dương là chiều từ A đến B .
- Theo bài ra ta có : \(\left\{{}\begin{matrix}x_1=30t\\x_2=L+40t\\x_{3.1}=L-50t\end{matrix}\right.\)
- Ta có : Khi xe 1 và xe 3 gặp nhau thì tổng quãng đường đi được là AB.
\(\Rightarrow80t=L\)
\(\Rightarrow t=\dfrac{L}{80}\)
=> Hai xe gặp nhau lại điểm cách A : \(\dfrac{30L}{80}=\dfrac{3L}{8}\left(km\right)\)
- Xét quá trình từ sau khi xe 1 gặp xe 3 :\(\left\{{}\begin{matrix}x_1=\dfrac{3L}{8}+30t^,\\x_2=40.\dfrac{L}{80}+L+40t^,\\x_3=\dfrac{3L}{8}+50t^,\end{matrix}\right.\)
- Để xe 2 đuổi kịp xe 3 thì \(\dfrac{3}{2}L+40t^,=\dfrac{3}{8}L+50t^,\)
Lại có : \(t=\dfrac{L}{80}\)
\(\Rightarrow t+t^,=0,09=\dfrac{L}{80}+t^,\)
- Giair hệ ta được : \(\left\{{}\begin{matrix}L=0,72\left(km\right)\\t^,=0,081\left(h\right)\\t=0,009\left(h\right)\end{matrix}\right.\)
b, Ta có : \(d_{3-1}=\dfrac{3}{8}L+50t^,-\dfrac{3}{8}L-30t^,=1,62\left(km\right)\)
Vậy ,....
- Gọi chiều dương là chiều từ người đi bộ hướng tới người đi xe đạp , thời gian gốc là to, điểm mốc tại người đi bộ và khoảng cách giữa người đi bộ và đi xe đạp là x0 ( km, x > 0 ) và 3 người xe đạp, bộ, xe máy lần lượt là 1,2,3 .
- Theo bài ra ta có : \(\left\{{}\begin{matrix}x_1=x_0+20t\\x_2=vt\\x_3=-2x_0+60t\end{matrix}\right.\)
- Để 3 người cùng gặp nhau tại 1 điểm .
=> \(x_1=x_2=x_3=x\)
\(\Rightarrow x_0=\dfrac{40}{3}t\)
\(\Rightarrow x=\dfrac{100}{3}t=vt\)
\(\Rightarrow v=\dfrac{100}{3}\left(km/h\right)\)
Vậy ...