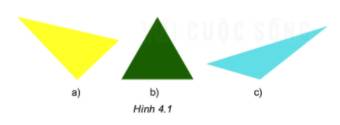
Chọn hình ảnh xuất hiện tam giác...
Đọc tiếp
Chọn hình ảnh xuất hiện tam giác đều.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
Q
6 tháng 4 2016
Lấy 3 còn lại 9 => nó là tg đều khi 2 đỉnh của tg phải cách nhau qua 3 đỉnh khác
Chia đỉnh đa giác thành 3 nhóm, mỗi nhóm có 4 đỉnh kề nhau, khi lấy 1 đỉnh ở nhóm này làm 1 đỉnh tg thì 2 đỉnh kia sẽ nằm tg ứng trong 2 nhóm còn lại, và số cách lấy 1 đỉnh trong 1 nhóm để làm đỉnh đa giác là 4 => có 4 tg đều có thể lập đc
=> Xác suất = ......
Nếu đã hiểu bài này, b có thể đưa ra 1 công thức: đó là nếu đa giác đều có 3n đỉnh (n thuộc N) thì số tam giác đều như trên là n
Chú ý chỉ là quan tâm đến chữ "đều" mà thôi, từ đó suy ra đc những tính chất mà đề yêu cầu, VD trong bài này, tính chất là mỗi đỉnh của tg đều pải cách nhau qua 3 đỉnh khác của đa giác, từ đó mới suy ra cách chọn ntn.
Còn công thức b co thể xem trên GL về tổ hợp xác suất trong hình học.
HQ
Hà Quang Minh
Giáo viên
3 tháng 10 2023
+ Trong hình 4.1 có hình b) là tam giác đều.
+ Một số hình ảnh thực tế: Hình biển báo giao thông, Mặt của khối rubic tam giác,...
CM
20 tháng 5 2019
Hình vuông là tứ giác đều (có bốn cạnh bằng nhau và các góc cùng bằng 900) và tam giác đều là những đa giác đều.
Hình chữ nhật là đa giác không đều vì hình chữ nhật có 4 góc vuông nhưng các cạnh không bằng nhau nên không là đa giác đều.
Hình thoi là đa giác không đều vì các cạnh bằng nhau nhưng các góc không bằng nhau.
Tam giác cân không là đa giác đều vì có ba cạnh không bằng nhau
Đáp án cần chọn là: B
HQ
Hà Quang Minh
Giáo viên
3 tháng 10 2023
Tam giác đều : biển báo giao thông, giá đựng sách, ...
Hình vuông : khuôn bánh chưng, gạch đá hoa, cửa sổ, ...
Hình lục giác đều: hộp mứt, giá sách, viên gạch lát nền,....
14 tháng 9 2021
Tam giác đều: cái cầu, biển báo,mái nhà, logo,...
Hình vuông: Gạch lát nền, rubik, bàn cờ, quân xúc xắc, mặt bàn,
Hình lục giác đều: tổ ong, biển báo, huy chương, ốc vít, bút chì, đồng hồ, mạng nhện, .
1 tháng 9 2021
Em tham khảo : ( Hoidap247 )
Bài thơ có kết cấu chặt chẽ theo lối đầu cuối tương ứng. Khi khổ mở đầu là “Mỗi năm hoa đào nỏ – Lại thấy ông đồ già” và kết thúc là “Năm nay đào lại nỏ – Không thấy ông đồ xưa”. Điều đó tập trung làm nổi bật chủ đề mang tinh thần hoài cổ cảnh đó người đâu. Màu thắm của hoa đào, màu đỏ của giấy, màu đen nhánh của mực tầu và mái tóc hoa râm của ông đồ trái ngược lại hoàn toàn với sự hiu hắt, buồn bã vắng vẻ ở những câu cuối. Ông đồ xuất hiện giữa một bức tranh lộng lẫy, ngoạn mục giữa phố xá tấp nập. Một vẻ đẹp sao vui tươi quá vậy! Ở khổ thơ đầu gợi lên cho độc giả niềm phấn chấn, tươi vui thì khổ cuối là một hình ảnh buồn bã, xót thương, sắc màu cũng phai nhạt theo. Giờ đây, ông đồ và lớp người xưa cũ đã trở nên vô nghĩa giữa cuộc đời. Bài thơ khép lại bằng những hình ảnh, câu thơ mang nặng nỗi buồn tha thiết của tác giả Vũ Đình Liên bằng câu hỏi tu từ. Mỗi năm đều mở đầu bằng hình ảnh hoa đào nhưng lòng người lại chả còn như xưa. Kết cấu đầu cuối tương ứng đã làm nổi bật được ý nghĩa và thông điệp của tác giả.
CM
7 tháng 6 2019
Đáp án C
+) Số tam giác được tạo từ 3 đỉnh trong 12 đỉnh: C 12 3
+) Số tam giác có 3 đỉnh là đỉnh của đa giác và 2 cạnh là cạnh của đa giác: cứ 3 đỉnh liên tiếp cho 1 tam giác thỏa mãn đề bài, nên có 12 tam giác
+) Số tam giác có 3 đỉnh là đỉnh của đa giác và 1 cạnh là cạnh của đa giác: cứ 1 cạnh, trừ đi 2 đỉnh kể, còn 8 đỉnh, với 2 đỉnh đầu mút của cạnh đó cho 1 tam giác thỏa mãn đề bài, nên có 8.12 tam giác
Vậy số tam giác có 3 đỉnh là đỉnh của đa giác và không có cạnh nào là cạnh của đa giác là C 12 3 − 12 − 8.12
Vậy kết quả là C 12 3 − 12 − 8.12 C 12 3
CM
19 tháng 7 2018
Đáp án C
+) Số tam giác được tạo từ 3 đỉnh trong 12 đỉnh: C 12 3
+) Số tam giác có 3 đỉnh là đỉnh của đa giác và 2 cạnh là cạnh của đa giác: cứ 3 đỉnh liên tiếp cho 1 tam giác thỏa mãn đề bài, nên có 12 tam giác
+) Số tam giác có 3 đỉnh là đỉnh của đa giác và 1 cạnh là cạnh của đa giác: cứ 1 cạnh, trừ đi 2 đỉnh kể, còn 8 đỉnh, với 2 đỉnh đầu mút của cạnh đó cho 1 tam giác thỏa mãn đề bài, nên có 8.12 tam giác
Vậy số tam giác có 3 đỉnh là đỉnh của đa giác và không có cạnh nào là cạnh của đa giác là C 12 3 - 12 - 12 . 8
Vậy kết quả là C 12 3 - 12 - 12 . 8 C 12 3
HQ
Hà Quang Minh
Giáo viên
3 tháng 10 2023
Hình ảnh có dạng hình lục giác đều: tổ ong, gạch lát nền, hộp bánh, ...
nhanh nha
Chọn hình ảnh xuất hiện tam giác đều.
Bên trên là 2 hình tam giác đều
Hok tốt